题目内容
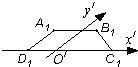 如图梯形A1B1C1D1是一平面图形ABCD的斜二侧直观图,若A1D1∥O′y′A1B1∥C1D1,A1B1=
如图梯形A1B1C1D1是一平面图形ABCD的斜二侧直观图,若A1D1∥O′y′A1B1∥C1D1,A1B1=| 2 |
| 3 |
分析:如图,根据直观图画法的规则,确定原平面图形四边形ABCD的形状,求出底边边长,上底边边长,以及高,然后求出面积.
解答: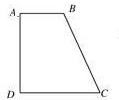 解:如图,根据直观图画法的规则,
解:如图,根据直观图画法的规则,
直观图中A1D1∥O′y′,A1D1=1,⇒原图中AD∥Oy,从而得出AD⊥DC,且AD=2A1D1=2,
直观图中A1B1∥C1D1,A1B1=
C1D1=2,⇒原图中AB∥CD,AB=
CD=2,
即四边形ABCD上底和下底边长分别为2,3,高为2,如图.
故其面积S=
(2+3)×2=5.
故选B.
 解:如图,根据直观图画法的规则,
解:如图,根据直观图画法的规则,直观图中A1D1∥O′y′,A1D1=1,⇒原图中AD∥Oy,从而得出AD⊥DC,且AD=2A1D1=2,
直观图中A1B1∥C1D1,A1B1=
| 2 |
| 3 |
| 2 |
| 3 |
即四边形ABCD上底和下底边长分别为2,3,高为2,如图.
故其面积S=
| 1 |
| 2 |
故选B.
点评:本题考查平面图形的直观图,考查计算能力,作图能力,是基础题.

练习册系列答案
 学期复习一本通学习总动员期末加暑假延边人民出版社系列答案
学期复习一本通学习总动员期末加暑假延边人民出版社系列答案 芒果教辅暑假天地重庆出版社系列答案
芒果教辅暑假天地重庆出版社系列答案
相关题目



 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.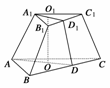
 (d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.
(d1+d2+d3)S,试判断V估与V的大小关系,并加以证明.

