题目内容
 (2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.
(2013•湖北)如图,某地质队自水平地面A,B,C三处垂直向地下钻探,自A点向下钻到A1处发现矿藏,再继续下钻到A2处后下面已无矿,从而得到在A处正下方的矿层厚度为A1A2=d1.同样可得在B,C处正下方的矿层厚度分别为B1B2=d2,C1C2=d3,且d1<d2<d3.过AB,AC的中点M,N且与直线AA2平行的平面截多面体A1B1C1-A2B2C2所得的截面DEFG为该多面体的一个中截面,其面积记为S中.(Ⅰ)证明:中截面DEFG是梯形;
(Ⅱ)在△ABC中,记BC=a,BC边上的高为h,面积为S.在估测三角形ABC区域内正下方的矿藏储量(即多面体A1B1C1-A2B2C2的体积V)时,可用近似公式V估=S中-h来估算.已知V=
| 1 | 3 |
分析:(Ⅰ)首先利用线面垂直、线面平行的性质及平行公理证出四边形DEFG的一组对边相互平行,然后由梯形中位线知识证明一组对边不相等,则可证明中截面DEFG是梯形;
(Ⅱ)由题意可证得MN是中截面梯形DEFG的高,根据四边形A1A2B2B1,A1A2C2C1均是梯形,利用梯形的中位线公式吧DE,FG用d1,d2,d3表示,这样就能把V估用含有a,h,d1,d2,d3的代数式表示,把V=
(d1+d2+d3)S与V估作差后利用d1,d2,d3的大小关系可以判断出差的符号,及能判断V估与V的大小关系.
(Ⅱ)由题意可证得MN是中截面梯形DEFG的高,根据四边形A1A2B2B1,A1A2C2C1均是梯形,利用梯形的中位线公式吧DE,FG用d1,d2,d3表示,这样就能把V估用含有a,h,d1,d2,d3的代数式表示,把V=
| 1 |
| 3 |
解答:(Ⅰ)依题意A1A2⊥平面ABC,B1B2⊥平面ABC,C1C2⊥平面ABC,
所以A1A2∥B1B2∥C1C2,又A1A2=d1,B1B2=d2,C1C2=d3,且d1<d2<d3.
因此四边形A1A2B2B1,A1A2C2C1均是梯形.
由AA2∥平面MEFN,AA2?平面AA2B2B,且平面AA2B2B∩平面MEFN=ME,
可得AA2∥ME,即A1A2∥DE.同理可证A1A2∥FG,所以DE∥FG.
又M,N分别为AB,AC的中点,
则D,E,F,G分别为A1B1,A2B2,A2C2,A1C1 的中点,
即DE、FG分别为梯形A1A2B2B1、A1A2C2C1的中位线.
因此DE=
(A1A2+B1B2)=
(d1+d2),FG=
(A1A2+C1C2)=
(d1+d3),
而d1<d2<d3,故DE<FG,所以中截面DEFG是梯形;
(Ⅱ)V估<V.证明:
由A1A2⊥平面ABC,MN?平面ABC,可得A1A2⊥MN.
而EM∥A1A2,所以EM⊥MN,同理可得FN⊥MN.
由MN是△ABC的中位线,可得MN=
BC=
a,即为梯形DEFG的高,
因此S中=S梯形DEFG=
(
+
)•
=
(2d1+d2+d3),
即V估=S中•h=
(2d1+d2+d3).又
S=
ah,所以V=
(d1+d2+d3)S=
(d1+d2+d3).
于是V-V估=
(d1+d2+d3)-
(2d1+d2+d3)=
[(d2-d1)+(d3-d1)].
由d1<d20,d3-d1>0,故V估<V.
所以A1A2∥B1B2∥C1C2,又A1A2=d1,B1B2=d2,C1C2=d3,且d1<d2<d3.
因此四边形A1A2B2B1,A1A2C2C1均是梯形.
由AA2∥平面MEFN,AA2?平面AA2B2B,且平面AA2B2B∩平面MEFN=ME,
可得AA2∥ME,即A1A2∥DE.同理可证A1A2∥FG,所以DE∥FG.
又M,N分别为AB,AC的中点,
则D,E,F,G分别为A1B1,A2B2,A2C2,A1C1 的中点,
即DE、FG分别为梯形A1A2B2B1、A1A2C2C1的中位线.
因此DE=
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
而d1<d2<d3,故DE<FG,所以中截面DEFG是梯形;
(Ⅱ)V估<V.证明:
由A1A2⊥平面ABC,MN?平面ABC,可得A1A2⊥MN.
而EM∥A1A2,所以EM⊥MN,同理可得FN⊥MN.
由MN是△ABC的中位线,可得MN=
| 1 |
| 2 |
| 1 |
| 2 |
因此S中=S梯形DEFG=
| 1 |
| 2 |
| d1+d2 |
| 2 |
| d1+d3 |
| 2 |
| a |
| 2 |
| a |
| 8 |
即V估=S中•h=
| ah |
| 8 |
S=
| 1 |
| 2 |
| 1 |
| 3 |
| ah |
| 6 |
于是V-V估=
| ah |
| 6 |
| ah |
| 8 |
| ah |
| 24 |
由d1<d20,d3-d1>0,故V估<V.
点评:本题考查直三棱柱的性质,体积,线面关系及空间想象能力,解答该题的关键是要有较强的空间想象能力,避免将各线面间的关系弄错,此题是中高档题.

练习册系列答案
相关题目
 (2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点.
(2013•湖北)如图,AB是圆O的直径,点C是圆O上异于A,B的点,直线PC⊥平面ABC,E,F分别是PA,PC的中点. (2013•湖北)如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )
(2013•湖北)如图,将一个各面都涂了油漆的正方体,切割为125个同样大小的小正方体,经过搅拌后,从中随机取一个小正方体,记它的涂漆面数为X,则X的均值E(X)=( )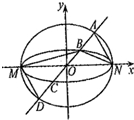 (2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记
(2013•湖北)如图,已知椭圆C1与C2的中心在坐标原点O,长轴均为MN且在x轴上,短轴长分别为2m,2n(m>n),过原点且不与x轴重合的直线l与C1,C2的四个交点按纵坐标从大到小依次为A,B,C,D,记