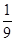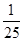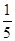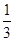题目内容
曲线C上任一点到定点(0,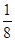 )的距离等于它到定直线
)的距离等于它到定直线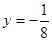 的距离.
的距离.
(1)求曲线C的方程;
(2)经过P(1,2)作两条不与坐标轴垂直的直线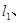
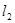 分别交曲线C于A、B两点,且
分别交曲线C于A、B两点,且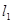 ⊥
⊥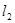 ,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
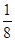 )的距离等于它到定直线
)的距离等于它到定直线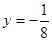 的距离.
的距离.(1)求曲线C的方程;
(2)经过P(1,2)作两条不与坐标轴垂直的直线
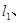
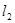 分别交曲线C于A、B两点,且
分别交曲线C于A、B两点,且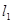 ⊥
⊥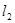 ,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.
,设M是AB中点,问是否存在一定点和一定直线,使得M到这个定点的距离与它到定直线的距离相等.若存在,求出这个定点坐标和这条定直线的方程.若不存在,说明理由.(1)y=2x2;
(2)M轨迹是抛物线,故存在一定点和一定直线,使得M到定点的距离等于它到定直线的距离。所求的定点为 ,定直线方程为y=
,定直线方程为y= .
.
(2)M轨迹是抛物线,故存在一定点和一定直线,使得M到定点的距离等于它到定直线的距离。所求的定点为
 ,定直线方程为y=
,定直线方程为y= .
.试题分析:
思路分析:(1)曲线C上任一点到定点(0,
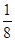 )的距离等于它到定直线
)的距离等于它到定直线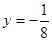 的距离.所以,由抛物线的定义,其方程为
的距离.所以,由抛物线的定义,其方程为 ,而
,而 ,所以,y=2x2;
,所以,y=2x2;(2)利用“参数法” 得到y=4x2+4x+
 ,根据图象的平移变换得到结论:定点为
,根据图象的平移变换得到结论:定点为 ,定直线方程为y=
,定直线方程为y= .
.解:(1)因为,利用抛物线的定义,确定得到y=2x2;
(2)设
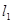 :y-2=k(x-1)(k≠0)
:y-2=k(x-1)(k≠0) 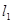 :y=2=
:y=2=
由
 得2x2-kx+k-2=0
得2x2-kx+k-2=0同理得B点坐标为

∴

消去k得:y=4x2+4x+
 ………9分
………9分M轨迹是抛物线,故存在一定点和一定直线,使得M到定点的距离等于它到定直线的距离。将抛物线方程化为
 ,此抛物线可看成是由抛物线
,此抛物线可看成是由抛物线 左移
左移 个单位,上移
个单位,上移 个单位得到的,而抛物线
个单位得到的,而抛物线 的焦点为(0,
的焦点为(0, ),准线为y=-
),准线为y=- .∴所求的定点为
.∴所求的定点为 ,定直线方程为y=
,定直线方程为y= .
.点评:难题,利用“直接法”可确定得到抛物线方程。利用“参数法”求得抛物线方程,通过研究焦点、准线等,达到确定“存在性”的目的。

练习册系列答案
相关题目
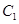 ,抛物线
,抛物线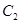 的焦点均在
的焦点均在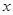 轴上,
轴上,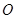 ,每条曲线上取两个点,将其坐标记录于表中:
,每条曲线上取两个点,将其坐标记录于表中:
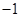
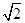
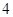
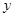
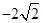
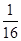
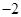
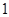
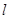 与
与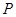 ,且与
,且与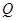 ,试探究:在坐标平面内是否存在定点
,试探究:在坐标平面内是否存在定点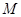 ,使得以
,使得以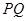 为直径的圆恒过点
为直径的圆恒过点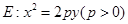 的焦点F作斜率分别为
的焦点F作斜率分别为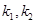 的两条不同的直线
的两条不同的直线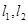 ,且
,且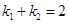 ,
,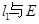 相交于点A,B,
相交于点A,B,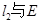 相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为
相交于点C,D。以AB,CD为直径的圆M,圆N(M,N为圆心)的公共弦所在的直线记为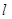 。
。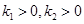 ,证明;
,证明;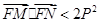 ;
;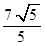 ,求抛物线E的方程。
,求抛物线E的方程。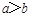 ,则
,则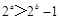 ”的否命题为“若
”的否命题为“若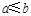 ,则
,则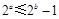 ”;
”;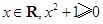 ”的否定是“存在
”的否定是“存在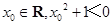 ”;
”;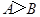 ”是“
”是“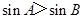 ”的充要条件.
”的充要条件.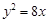 上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )
上一点P到y轴的距离是4,则点P到该抛物线焦点的距离是( )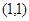 的抛物线的标准方程是 .
的抛物线的标准方程是 .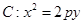 (
(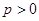 )上一点
)上一点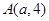 到其准线的距离为
到其准线的距离为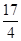 .
.
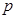 与
与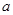 的值;
的值;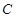 上动点
上动点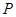 的横坐标为
的横坐标为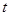 (
(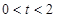 ),过点
),过点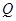 ,交
,交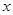 轴于
轴于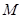 点(直线
点(直线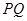 的斜率记作
的斜率记作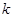 ).过点
).过点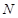 .若
.若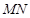 恰好是
恰好是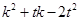 是否为定值?若是,求出该定值;若不是,说明理由.
是否为定值?若是,求出该定值;若不是,说明理由.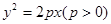 上一点
上一点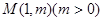 到其焦点的距离为5,双曲线
到其焦点的距离为5,双曲线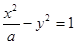 的左顶点为
的左顶点为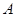 ,若双曲线的一条渐近线与直线
,若双曲线的一条渐近线与直线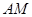 平行,则实数
平行,则实数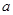 的值是( )
的值是( )