题目内容
【题目】在△ABC中，角A，B，C所对的边分别是a，b，c，且csin2B﹣bsin（A+B）＝0
（1）求角B的大小；
（2）设a＝4，c＝6，求sinC的值．
【答案】（1）
（2）
【解析】
（1）根据正弦定理得到sinCsin2B﹣sinBsin（A+B）＝0，化简得到cosB
，解得答案.
（2）根据余弦定理得到b＝2
，再根据正弦定理计算得到答案.
∵csin2B﹣bsin（A+B）＝0，由正弦定理可得，sinCsin2B﹣sinBsin（A+B）＝0，
化简可得2sinCsinBcosB﹣sinBsinC＝0，∵sinBsinC≠0，∴cosB，
∵B∈（0，π），∴
.
（2）由余弦定理可得：cosB
，
，∴b＝2，
由正弦定理可得：sinC
.
练习册系列答案
相关题目
【题目】某大型商场的空调在1月到5月的销售量与月份相关，得到的统计数据如下表：
月份 | 1 | 2 | 3 | 4 | 5 |
销量 | 0.6 | 0.8 | 1.2 | 1.6 | 1.8 |
（1）经分析发现1月到5月的销售量可用线性回归模型拟合该商场空调的月销量
（百件）与月份
之间的相关关系.请用最小二乘法求关于的线性回归方程
，并预测6月份该商场空调的销售量；
（2）若该商场的营销部对空调进行新一轮促销，对7月到12月有购买空调意愿的顾客进行问卷调查.假设该地拟购买空调的消费群体十分庞大，经过营销部调研机构对其中的500名顾客进行了一个抽样调查，得到如下一份频数表：
有购买意愿对应的月份 | 7 | 8 | 9 | 10 | 11 | 12 |
频数 | 60 | 80 | 120 | 130 | 80 | 30 |
现采用分层抽样的方法从购买意愿的月份在7月与12月的这90名顾客中随机抽取6名，再从这6人中随机抽取3人进行跟踪调查，求抽出的3人中恰好有2人是购买意愿的月份是12月的概率.
参考公式与数据：线性回归方程，其中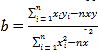
，
.
