题目内容
设X~N(1,22),试求
(1)P(-1<X≤3);
(2)P(3<X≤5);
(3)P(X≥5).
(1)P(-1<X≤3);
(2)P(3<X≤5);
(3)P(X≥5).
(1)0.682 6(2)0.135 9(3)0.022 8
∵X~N(1,22),∴ =1,
=1, =2.
=2.
(1)P(-1<X≤3)=P(1-2<X≤1+2)=P( -
- <X≤
<X≤ +
+ )="0.682" 6.
)="0.682" 6.
(2)∵P(3<X≤5)=P(-3<X≤-1)
∴P(3<X≤5)= [P(-3<X≤5)-P(-1<X≤3)]=
[P(-3<X≤5)-P(-1<X≤3)]= [P(1-4<X≤1+4)-P(1-2<X≤1+2)]
[P(1-4<X≤1+4)-P(1-2<X≤1+2)]
= [P(
[P( -2
-2 <X≤
<X≤ +2
+2 )-P(
)-P( -
- <X≤
<X≤ +
+ )]=
)]= ×(0.954 4-0.682 6)="0.135" 9.
×(0.954 4-0.682 6)="0.135" 9.
(3)∵P(X≥5)=P(X≤-3),
∴P(X≥5)= [1-P(-3<X≤5)]=
[1-P(-3<X≤5)]= [1-P(1-4<X≤1+4)]
[1-P(1-4<X≤1+4)]
= [1-P(
[1-P( -2
-2 <X≤
<X≤ +2
+2 )]=
)]= (1-0.954 4)="0.022" 8.
(1-0.954 4)="0.022" 8.
 =1,
=1, =2.
=2.(1)P(-1<X≤3)=P(1-2<X≤1+2)=P(
 -
- <X≤
<X≤ +
+ )="0.682" 6.
)="0.682" 6.(2)∵P(3<X≤5)=P(-3<X≤-1)
∴P(3<X≤5)=
 [P(-3<X≤5)-P(-1<X≤3)]=
[P(-3<X≤5)-P(-1<X≤3)]= [P(1-4<X≤1+4)-P(1-2<X≤1+2)]
[P(1-4<X≤1+4)-P(1-2<X≤1+2)]=
 [P(
[P( -2
-2 <X≤
<X≤ +2
+2 )-P(
)-P( -
- <X≤
<X≤ +
+ )]=
)]= ×(0.954 4-0.682 6)="0.135" 9.
×(0.954 4-0.682 6)="0.135" 9.(3)∵P(X≥5)=P(X≤-3),
∴P(X≥5)=
 [1-P(-3<X≤5)]=
[1-P(-3<X≤5)]= [1-P(1-4<X≤1+4)]
[1-P(1-4<X≤1+4)]=
 [1-P(
[1-P( -2
-2 <X≤
<X≤ +2
+2 )]=
)]= (1-0.954 4)="0.022" 8.
(1-0.954 4)="0.022" 8.
练习册系列答案
相关题目
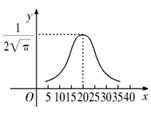
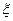 服从
服从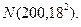
 )(单位
)(单位 ).今从甲乙两箱成品中各随机抽取一个电阻,测得阻值分别为1011
).今从甲乙两箱成品中各随机抽取一个电阻,测得阻值分别为1011 ~
~ ,且
,且 ,则
,则 的方差为 .
的方差为 .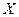 服从标准正态分布
服从标准正态分布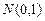 ,
,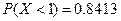 ,则
,则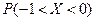 等于( )
等于( )



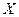 服从正态分布
服从正态分布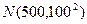 ,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中
,现有2500名考生,据往年录取率可推测今年约有1000名高考考生考上一类大学,估计今年一类大学的录取分数线为 分.(其中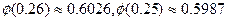 )
)