Question

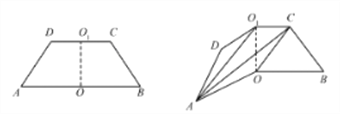
【题目】如图，某地三角工厂分别位于边长为2的正方形的两个顶点及中点处.为处理这三角工厂的污水，在该正方形区域内（含边界）与等距的点处建一个污水处理厂，并铺设三条排污管道，记辅设管道总长为千米.

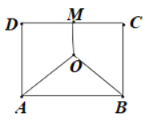
（1）按下列要求建立函数关系式：

（i）设，将表示成的函数；

（ii）设，将表示成的函数；

（2）请你选用一个函数关系，确定污水厂位置，使铺设管道总长最短.

Answer 1

【答案】（1）（i）（，其中）.（ii).

（2）污水厂设在与直线距离处

【解析】

（1）（i）设的中点为，则，，，，由此可得关于的函数；

（ii）由题意，则，，由此可得关于的函数；

（2）设，，则，然后利用基本不等式求最值．

解：

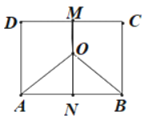
（1）（i）设中点，则，，，，

∴（，其中）；

（ii），，

；

（2）设，，则，

，

当，即时，取最小值，

∴污水厂设在与直线距离处时，铺设管道总长最短，最短长度为千米．