题目内容
设
A、B是x轴上的两点，点P的横坐标为2，且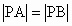
，若直线PA的方程为x－y＋1=0，则直线PB的方程为
[
]|
A ．x＋y－5=0 |
B ．2x－y－1=0 |
|
C ．2y－x－4=0 |
D ．2x＋y－7=0 |
答案：A
解析：
提示：
解析：
|
解：由 PA的方程x－y＋1=0，且点A在x轴上，点P的横坐标为2，可知A(－1，0)，P(2，3)．由于点 B在x轴上，可设其坐标为(t，0)，∵PA| ＝|PB|，∴ ，
解得 t=5或t=－1(舍去)．∴ 点B的坐标为(5，0)．由两点式得 PB所在的直线方程为 ，
即 x＋y－5=0．∴选A． |
提示：
|
本题考查直线方程的求法． 本题已知 PA所在直线的方程，便可求出点P、A的坐标，且|PA|＝|PB|建立关于B点坐标的关系式，求出点B的坐标即可． |
练习册系列答案
相关题目