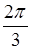题目内容
已知函数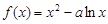 在
在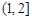 是增函数,
是增函数,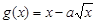 在(0,1)为减函数.
在(0,1)为减函数.
(I)求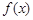 、
、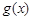 的表达式;
的表达式;
(II)求证:当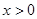 时,方程
时,方程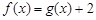 有唯一解;
有唯一解;
(Ⅲ)当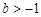 时,若
时,若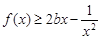 在
在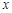 ∈
∈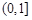 内恒成立,求
内恒成立,求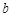 的取值范围.
的取值范围.
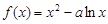 在
在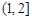 是增函数,
是增函数,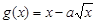 在(0,1)为减函数.
在(0,1)为减函数.(I)求
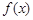 、
、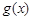 的表达式;
的表达式;(II)求证:当
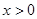 时,方程
时,方程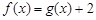 有唯一解;
有唯一解;(Ⅲ)当
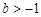 时,若
时,若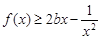 在
在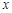 ∈
∈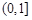 内恒成立,求
内恒成立,求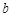 的取值范围.
的取值范围.(I)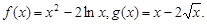 (II)由(1)可知,方程
(II)由(1)可知,方程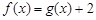 ,
,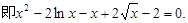
设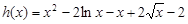 ,
,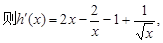
令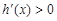 ,并由
,并由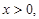 得
得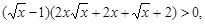 解知
解知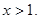 ;(III)
;(III)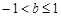
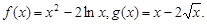 (II)由(1)可知,方程
(II)由(1)可知,方程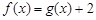 ,
,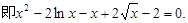
设
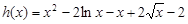 ,
,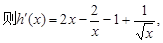
令
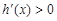 ,并由
,并由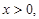 得
得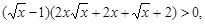 解知
解知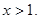 ;(III)
;(III)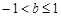
试题分析:(I)
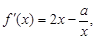 依题意
依题意 ,即
,即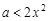 ,
,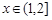 .
.∵上式恒成立,∴
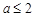 ① …………………………1分
① …………………………1分又
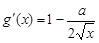 ,依题意
,依题意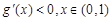 ,即
,即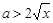 ,
,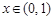 .
.∵上式恒成立,∴
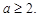 ② …………………………2分
② …………………………2分由①②得
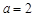 . …………………………3分
. …………………………3分∴
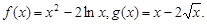 …………………………4分
…………………………4分(II)由(1)可知,方程
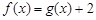 ,
,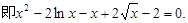
设
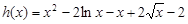 ,
,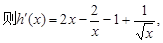
令
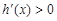 ,并由
,并由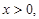 得
得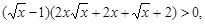 解知
解知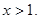 ………5分
………5分令
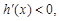 由
由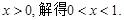 …………………………6分
…………………………6分列表分析:
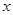 | (0,1) | 1 | (1,+¥) |
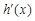 | - | 0 | + |
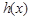 | 递减 | 0 | 递增 |
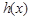 在
在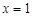 处有一个最小值0, …………………………7分
处有一个最小值0, …………………………7分当
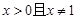 时,
时,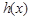 >0,∴
>0,∴ 在(0,+¥)上只有一个解.
在(0,+¥)上只有一个解.即当x>0时,方程
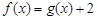 有唯一解. ……………………8分
有唯一解. ……………………8分(III)设
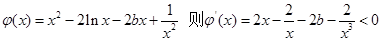 , ……9分
, ……9分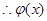 在
在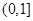 为减函数
为减函数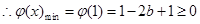 又
又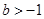 …………11分
…………11分所以:
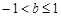 为所求范围. ………………12分
为所求范围. ………………12分点评:导数的应用是高考的一个重点,利用导数求最值及判断函数的单调性比用定义法要简单的多,要注意利用这个工具

练习册系列答案
 导学与测试系列答案
导学与测试系列答案 新非凡教辅冲刺100分系列答案
新非凡教辅冲刺100分系列答案
相关题目
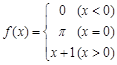 ,则
,则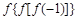 =( )
=( )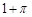
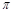
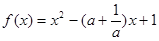 ,
,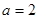 时,解不等式
时,解不等式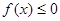 ;
;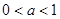 ,解关于
,解关于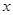 的不等式
的不等式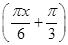 (0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.
(0≤x≤5),点A、B分别是函数y=f(x)图像上的最高点和最低点.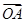 ·
·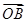 的值;
的值;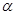 、
、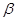 的终边上,求tan(
的终边上,求tan(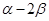 )的值.
)的值.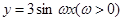 在区间
在区间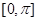 恰有2个零点,则
恰有2个零点,则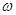 的取值范围是( )
的取值范围是( )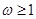
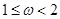
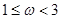
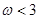
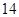 分)已知函数
分)已知函数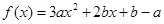 (
(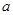 ,
,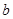 是不同时为零的常数).
是不同时为零的常数).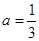 时,若不等式
时,若不等式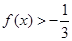 对任意
对任意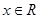 恒成立,求实数
恒成立,求实数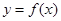 在
在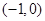 内至少存在一个零点.
内至少存在一个零点. 的零点一定位于区间( )
的零点一定位于区间( )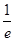 ,1)
,1)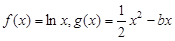 (
(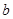 为常数)。
为常数)。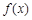 的图象在点(
的图象在点(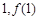 )处的切线与函数
)处的切线与函数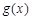 的图象相切,求实数
的图象相切,求实数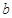 的值;
的值;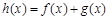 ,若函数
,若函数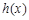 在定义域上存在单调减区间,求实数
在定义域上存在单调减区间,求实数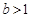 ,对于区间[1,2]内的任意两个不相等的实数
,对于区间[1,2]内的任意两个不相等的实数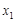 ,
,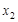 ,都有
,都有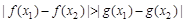 成立,求
成立,求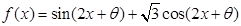 的图像关于原点对称,且满足对于
的图像关于原点对称,且满足对于 内任意两个数
内任意两个数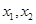 ,恒有
,恒有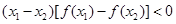 的
的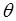 的一个取值可以是( )
的一个取值可以是( )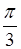 B.
B.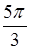 C.
C.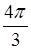 D.
D.