题目内容
18．已知F1、F2是椭圆的两个焦点，A是椭圆的一个短轴端点，直线AF1、AF2分别与椭圆交于B、C（不同于点A），若△ABC为正三角形，则这个椭圆的离心率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{3}}{2}$ | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{6}}{3}$ |
分析 如图所示，由△ABC为正三角形，根据椭圆的对称性可得：△AF1F2也是正三角形．即可得出．
解答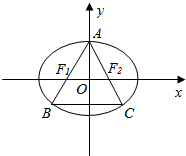 
解：如图所示，
∵△ABC为正三角形，
根据椭圆的对称性可得：△AF1F2也是正三角形．
∴a=|AF1|=2|OF1|=2c，
∴离心率e=$\frac{c}{a}$=$\frac{1}{2}$．
故选：A．
点评 本题考查了椭圆的标准方程及其性质、正三角形的性质，考查了推理能力与计算能力，属于中档题．
练习册系列答案
相关题目