题目内容
已知数列{an}满足Sn+an=2n+1, (1) 写出a1, a2, a3,并推测an的表达式;
(2) 用数学归纳法证明所得的结论。
(2) 用数学归纳法证明所得的结论。
(1) a1=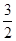 , a2=
, a2=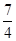 , a3=
, a3= ,
,
猜测 an=2-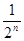
(2)证明: ①由(1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-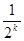 ,
,
当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-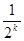 , ak+1=2-
, ak+1=2-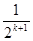 , 即当n=k+1时,命题成立.
, 即当n=k+1时,命题成立.
综合(1),(2)可知:对于任意正整数n,都有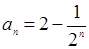
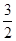 , a2=
, a2=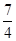 , a3=
, a3= ,
, 猜测 an=2-
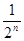
(2)证明: ①由(1)已得当n=1时,命题成立;
②假设n=k时,命题成立,即 ak=2-
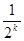 ,
, 当n=k+1时, a1+a2+……+ak+ak+1+ak+1=2(k+1)+1,
且a1+a2+……+ak=2k+1-ak
∴2k+1-ak+2ak+1=2(k+1)+1=2k+3,
∴2ak+1=2+2-
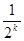 , ak+1=2-
, ak+1=2-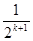 , 即当n=k+1时,命题成立.
, 即当n=k+1时,命题成立. 综合(1),(2)可知:对于任意正整数n,都有
略

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
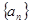 的公差d不为0,
的公差d不为0,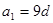 ,若
,若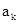 是
是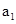 与
与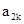 的等比中项,则k=( )
的等比中项,则k=( )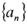 中a1=2,点
中a1=2,点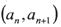 在函数
在函数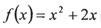 的图象上,
的图象上,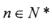 .数列
.数列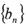 的前n项和为Sn,且满足b1=1,当n
的前n项和为Sn,且满足b1=1,当n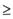 2时,
2时,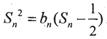 .
.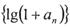 是等比数列;
是等比数列;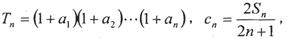 求
求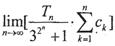 的值.
的值.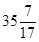 ,则插去的那个数为( ).
,则插去的那个数为( ).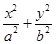 =1(a>b>0)的左、右焦点为F1、F2,e=
=1(a>b>0)的左、右焦点为F1、F2,e=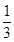 ,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。
,过F1的直线l交椭圆C于A、B两点,|AF2|、|AB|、|BF2|成等差数列,且|AB|=4。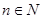 ,满足以下性质:(1)2&2=1,(2)(
,满足以下性质:(1)2&2=1,(2)(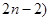 &2=(
&2=(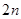 &2)+3,则2008&2的数值为
&2)+3,则2008&2的数值为 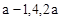 ,记前n项和为Sn
,记前n项和为Sn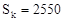 ,求a和k的值;
,求a和k的值;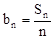 ,求
,求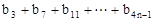 的值
的值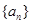 中,
中,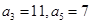 ,问
,问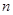 为何值时
为何值时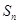 取得最大值,并求最大值
取得最大值,并求最大值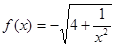 ,数列
,数列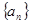 的前
的前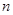 项和为
项和为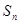 ,点
,点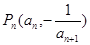 在曲线
在曲线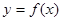 上
上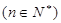 ,
,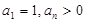
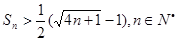 ,
,