题目内容
14.若函数f(x)=-x2-x,g(x)=x2-5x+5,则f(g(x))的值域为( )| A. | (-∞,$\frac{1}{4}$) | B. | (-∞,$\frac{1}{4}$] | C. | [-$\frac{1}{4}$,$\frac{1}{4}$] | D. | ($\frac{1}{4}$,+∞) |
分析 对g(x)配方,$g(x)=(x-\frac{5}{2})^{2}-\frac{5}{4}≥-\frac{5}{4}$,可换元,令g(x)=t,这样对f(t)配方,然后求该函数在t$≥-\frac{5}{4}$上的值域即可得出原函数的值域.
解答 解:g(x)=${x}^{2}-5x+5=(x-\frac{5}{2})^{2}-\frac{5}{4}≥-\frac{5}{4}$;
令g(x)=t,t$≥-\frac{5}{4}$;
∴$f(t)=-(t+\frac{1}{2})^{2}+\frac{1}{4}$≤$\frac{1}{4}$;
∴原函数的值域为(-∞,$\frac{1}{4}$].
故选:B.
点评 考查函数值域的概念,配方法求二次函数的值域,换元方法求函数的值域,要熟悉二次函数的图象.

练习册系列答案
相关题目
6.函数f(x)=asin2x+b${x}^{\frac{2}{3}}$+c(a,b∈R),若f(-2015)=2013,则f(2015)=( )
| A. | 2018 | B. | -2009 | C. | 2013 | D. | -2013 |
19.若定义在R上的奇函数f(x)在(-∞,0)上是减函数,且x1+x2>0,x2+x3>0,x3+x1>0,f(x1)+f(x2)+f(x3)的值( )
| A. | 大于0 | B. | 小于0 | C. | 等于0 | D. | 大于或等于0 |
6.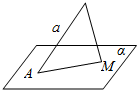 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
 已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )
已知AB是面α的斜线段,斜足为A,AB=a,点M是面α内的动点,△ABM的面积为定值b,则点M的轨迹是( )| A. | 线段 | B. | 椭圆 | C. | 双曲线 | D. | 抛物线 |
1.集合A={a,b},其中非空真子集个数是( )
| A. | 1 | B. | 2 | C. | 3 | D. | 4 |