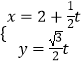题目内容
【题目】某工厂生产一种机器的固定成本为5000元，且每生产100部，需要加大投入2500元．对销售市场进行调查后得知，市场对此产品的需求量为每年500部，已知销售收入函数为 
，其中x是产品售出的数量0≤x≤500．
（1）若为x年产量，y表示利润，求y=f（x）的解析式
（2）当年产量为何值时，工厂的年利润最大？其最大值是多少？
【答案】
（1）解：利润等于销售收入（ 
）减去成本（25x+5000），
故 
，（0≤x≤500）；
（2）利用二次函数的性质可得，当x=475时，函数y=f（x）取得最大值为 
（元），
即：当年产量为475部时，工厂的年利润最大，其最大值为： 元．
【解析】（1）由题意可列出函数的解析式。（2）根据二次函数最值得情况求出结果。
【考点精析】认真审题，首先需要了解二次函数在闭区间上的最值(当
时，当
时，
；当
时在
上递减，当时，
)．
练习册系列答案
相关题目
