题目内容
20.关于x的方程$\sqrt{2}$sin(x+$\frac{π}{4}$)=2m在[0,π]内有相异两实根,则实数m的取值范围为[$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$).分析 由题意可得,函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)的图象和直线y=2m在[0,π]内有相异的两个交点,数形结合可得实数m的取值范围.
解答 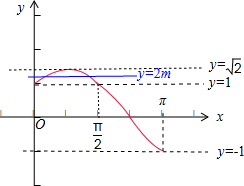 解:由题意可得,函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)的图象
解:由题意可得,函数y=$\sqrt{2}$sin(x+$\frac{π}{4}$)的图象
和直线y=2m在[0,π]内有相异的两个交点.
由x∈[0,π],可得x+$\frac{π}{4}$[$\frac{π}{4}$,$\frac{5π}{4}$],sin(x+$\frac{π}{4}$)∈[-$\frac{\sqrt{2}}{2}$,1],$\sqrt{2}$sin(x+$\frac{π}{4}$)∈[-1,$\sqrt{2}$],
数形结合求得实数2m的取值范围为[1,$\sqrt{2}$),故实数m的取值范围为[$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$),
故答案为:[$\frac{1}{2}$,$\frac{\sqrt{2}}{2}$).
点评 本题主要考查正弦函数的图象特征,方程根的存在性以及个数判断,体现了转化、数形结合的数学思想,属于中档题.

练习册系列答案
相关题目
11.与直线x+2y-4=0在x轴上的截距相同,与直线xtan$\frac{2π}{3}$+y-4=0的倾斜角相同的直线方程为( )
| A. | $\sqrt{3}$x-y-4=0 | B. | $\sqrt{3}$x-y-4$\sqrt{3}$=0 | C. | $\sqrt{3}$x+y-4=0 | D. | $\sqrt{3}$x+y-4$\sqrt{3}$=0 |
12.已知矩形ABCD,AB=6,BC=4,经过A、B、C、D四顶点的椭圆(BC经过椭圆的焦点)的离心率是( )
| A. | $\frac{3}{4}$ | B. | $\frac{1}{2}$ | C. | $\frac{2}{3}$ | D. | $\frac{3}{1+\sqrt{10}}$ |
 如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.
如图,抛物线关于x轴对称,它的顶点在坐标原点,点P(1,2)、A(x1,y1)、B(x2,y2)均在抛物线上.