题目内容
已知函数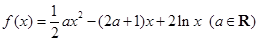 .
.
(1)若曲线 在
在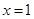 和
和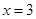 处的切线互相平行,求
处的切线互相平行,求 的值;
的值;
(2)求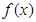 的单调区间;
的单调区间;
(3)设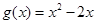 ,若对任意
,若对任意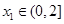 ,均存在
,均存在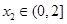 ,使得
,使得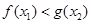 ,求
,求 的取值范围.
的取值范围.
【答案】
(1) . (2) ①当
. (2) ①当 时,
时,  的单调递增区间是
的单调递增区间是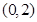 ,单调递减区间是
,单调递减区间是 . ②当
. ②当 时,
时,  的单调递增区间是
的单调递增区间是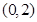 和
和 ,单调递减区间是
,单调递减区间是 . (3)
. (3) .
.
【解析】
试题分析:
 .
.
(1)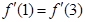 ,解得
,解得 .
.
(2)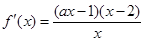
 .
.
①当 时,
时,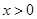 ,
,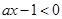 ,
,
在区间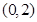 上,
上,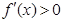 ;在区间
;在区间 上
上 ,
,
故 的单调递增区间是
的单调递增区间是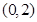 ,单调递减区间是
,单调递减区间是 .
.
②当 时,
时, ,
,
在区间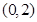 和
和 上,
上,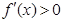 ;在区间
;在区间 上
上 ,
,
故 的单调递增区间是
的单调递增区间是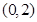 和
和 ,单调递减区间是
,单调递减区间是 .
.
③当 时,
时,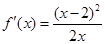 , 故
, 故 的单调递增区间是
的单调递增区间是 .
.
④当 时,
时, ,
,
在区间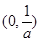 和
和 上,
上,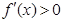 ;在区间
;在区间 上
上 ,
,
故 的单调递增区间是
的单调递增区间是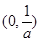 和
和 ,单调递减区间是
,单调递减区间是 .
.
(3)由已知,在 上有
上有 .
.
由已知, ,由(2)可知,
,由(2)可知,
①当 时,
时, 在
在 上单调递增,
上单调递增,
故 ,
,
所以, ,解得
,解得 ,故
,故 .
.
②当 时,
时, 在
在 上单调递增,在
上单调递增,在 上单调递减,
上单调递减,
故 .
.
由 可知
可知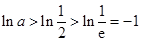 ,
, ,
,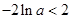 ,
,
所以, ,
, ,
,
综上所述, .
.
考点:本题考查了导数的运用
点评:对于函数与导数这一综合问题的命制,一般以有理函数与半超越(指数、对数)函数的组合复合且含有参量的函数为背景载体,解题时要注意对数式对函数定义域的隐蔽,这类问题重点考查函数单调性、导数运算、不等式方程的求解等基本知识,注重数学思想方法的运用.

练习册系列答案
相关题目
 :
: 上存在零点,求实数
上存在零点,求实数 的取值范围;
的取值范围; ,当
,当 时,
时, 的值域为区间
的值域为区间 ,且
,且 .
. ,
, ,
, ,且
,且 的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点(
的定义域是[– 1,1],P(x1,y1),Q(x2,y2)是其图象上任意两点( ),设直线PQ的斜率为k,求证:
),设直线PQ的斜率为k,求证: ;
; ,且
,且 ,
, .
. .
. .
. ,求a的取值范围;
,求a的取值范围; .
. .
. 在x = 0处取得极值为 – 2,求a、b的值;
在x = 0处取得极值为 – 2,求a、b的值; 上是增函数,求实数a的取值范围.
上是增函数,求实数a的取值范围.