题目内容
已知圆C:x2+y2-4x-2y+1=0,直线l:3x-4y+k=0圆上存在两点到直线l的距离为1,则k的取值范围是
- A.(-17,-7)
- B.(3,13)
- C.(-17,-7)∪(3,13)
- D.[-17,-7]∪[3,13]
C
分析:先求出圆心和半径,再设过圆心C(2,1)且平行于直线l:3x-4y+k=0的直径所在的直线方程是3x-4y-2=0,直线3x-4y-2=0与直线l:3x-4y+k=0的距离是d=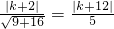 ,由题设条件知
,由题设条件知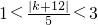 ,由此可知k的取值范围.
,由此可知k的取值范围.
解答:由题设知圆心C(2,1),半径r=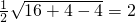 ,
,
过圆心C(2,1)且平行于直线l:3x-4y+k=0的直径所在的直线方程是3x-4y-2=0,
直线3x-4y-2=0与直线l:3x-4y+k=0的距离是d=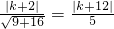 ,
,
由题设条件知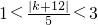 ,
,
解得k∈(-17,-7)∪(3,13).
故选C.
点评:本题考查直线和圆的位置关系,解题时要注意两条平行线的距离公式的合理运用.
分析:先求出圆心和半径,再设过圆心C(2,1)且平行于直线l:3x-4y+k=0的直径所在的直线方程是3x-4y-2=0,直线3x-4y-2=0与直线l:3x-4y+k=0的距离是d=
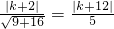 ,由题设条件知
,由题设条件知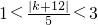 ,由此可知k的取值范围.
,由此可知k的取值范围.解答:由题设知圆心C(2,1),半径r=
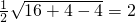 ,
,过圆心C(2,1)且平行于直线l:3x-4y+k=0的直径所在的直线方程是3x-4y-2=0,
直线3x-4y-2=0与直线l:3x-4y+k=0的距离是d=
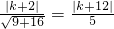 ,
,由题设条件知
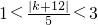 ,
,解得k∈(-17,-7)∪(3,13).
故选C.
点评:本题考查直线和圆的位置关系,解题时要注意两条平行线的距离公式的合理运用.

练习册系列答案
相关题目
 (2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.
(2009•普陀区一模)如图,已知圆C:x2+y2=r2与x轴负半轴的交点为A.由点A出发的射线l的斜率为k,且k为有理数.射线l与圆C相交于另一点B.