题目内容
(2012•泸州一模)已知圆C:x2+y2=r2(r>0)与抛物线y2=40x的准线相切,若直线l:
+
=1与圆C有公共点,且公共点都为整点(整点是指横坐标.纵坐标都是整数的点),那么直线l共有( )
| x |
| a |
| y |
| b |
分析:由题意可求r=10,从而可求出x2+y2=100上的整点个数,共12个点,由题意可知直线
+
=1(a,b为非零实数)与x,y轴不平行,不经过原点,求出所有的直线的条数,去掉不满足题意的直线的条数即可.
| x |
| a |
| y |
| b |
解答: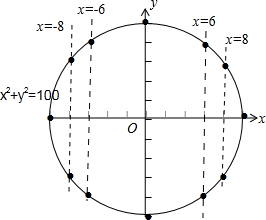 解:∵圆C:x2+y2=r2(r>0)与抛物线y2=40x的准线x=-10相切,
解:∵圆C:x2+y2=r2(r>0)与抛物线y2=40x的准线x=-10相切,
∴r=10,
∴圆C的方程为:x2+y2=100.
∴圆x2+y2=100上的整点为(0,±10),(±6,±8),(±8,±6),(±10,0),共12个点,
∵直线
+
=1(a,b为非零实数),
∴直线与x,y轴不平行,不经过原点,
①过每个整点都有一条圆的切线,共12条,不符合要求的4条,分别是过与坐标轴的交点的切线;
②又任意两点连线有
条,
过圆上两整点与x,y轴平行的有8条(x=±6,±8,y=±6,±8),暂不包括x轴与y轴;
经过原点的有6条(包括x轴与y轴),
综①②知,符合条件的直线共有
+(12-4)-8-6=60.
故选A.
 解:∵圆C:x2+y2=r2(r>0)与抛物线y2=40x的准线x=-10相切,
解:∵圆C:x2+y2=r2(r>0)与抛物线y2=40x的准线x=-10相切,∴r=10,
∴圆C的方程为:x2+y2=100.
∴圆x2+y2=100上的整点为(0,±10),(±6,±8),(±8,±6),(±10,0),共12个点,
∵直线
| x |
| a |
| y |
| b |
∴直线与x,y轴不平行,不经过原点,
①过每个整点都有一条圆的切线,共12条,不符合要求的4条,分别是过与坐标轴的交点的切线;
②又任意两点连线有
| C | 2 12 |
过圆上两整点与x,y轴平行的有8条(x=±6,±8,y=±6,±8),暂不包括x轴与y轴;
经过原点的有6条(包括x轴与y轴),
综①②知,符合条件的直线共有
| C | 2 12 |
故选A.
点评:本题考查直线与圆的综合运用,解题时要认真审题,仔细解答,注意挖掘题设中的隐含条件,合理地进行等价转化,恰当地借助数形结合进行求解,属于难题.

练习册系列答案
相关题目
 (2012•泸州一模)用一个边长为
(2012•泸州一模)用一个边长为 (2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,
(2012•泸州一模)如图,在直三棱柱ABC-A′B′C′中,AB=BC=CA=a,