题目内容
已知长方体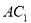 中,
中, ,
,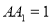 ,
,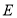 为
为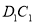 的中点,如图所示.
的中点,如图所示.
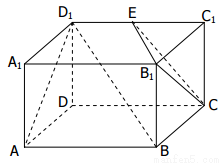
(1)在所给图中画出平面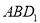 与平面
与平面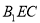 的交线(不必说明理由);
的交线(不必说明理由);
(2)证明: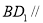 平面
平面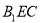 ;
;
(3)求平面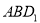 与平面
与平面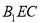 所成锐二面角的大小.
所成锐二面角的大小.
练习册系列答案
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案
相关题目
题目内容
已知长方体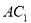 中,
中, ,
,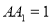 ,
,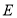 为
为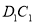 的中点,如图所示.
的中点,如图所示.

(1)在所给图中画出平面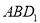 与平面
与平面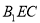 的交线(不必说明理由);
的交线(不必说明理由);
(2)证明: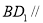 平面
平面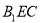 ;
;
(3)求平面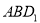 与平面
与平面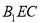 所成锐二面角的大小.
所成锐二面角的大小.
 暑假作业海燕出版社系列答案
暑假作业海燕出版社系列答案 本土教辅赢在暑假高效假期总复习云南科技出版社系列答案
本土教辅赢在暑假高效假期总复习云南科技出版社系列答案 暑假作业北京艺术与科学电子出版社系列答案
暑假作业北京艺术与科学电子出版社系列答案