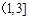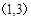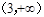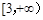题目内容
曲线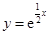 在点
在点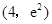 处的切线与坐标轴所围三角形的面积为( )
处的切线与坐标轴所围三角形的面积为( )
A.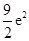 | B.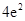 | C.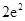 | D.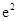 |
D
解析试题分析: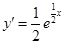 ,切线的斜率k=
,切线的斜率k=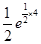 =
=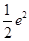 ,所以切线方程为y=
,所以切线方程为y=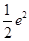 (x-4)+e2,切线与坐标轴的交点为(0,-e2),(2,0),所以切线与坐标轴所围三角形的面积为
(x-4)+e2,切线与坐标轴的交点为(0,-e2),(2,0),所以切线与坐标轴所围三角形的面积为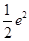 ×2=
×2=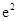 ,故选D.
,故选D.
考点:1.函数导数的几何意义;2.三角形面积.

练习册系列答案
相关题目
如果函数 满足:对于任意的
满足:对于任意的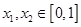 ,都有
,都有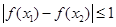 恒成立,则
恒成立,则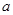 的取值范围是( )
的取值范围是( )
A.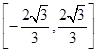 | B. |
C.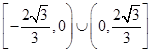 | D.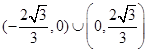 |
已知函数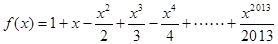 ,
,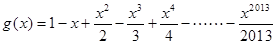 ,设函数
,设函数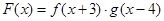 ,且函数
,且函数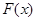 的零点均在区间
的零点均在区间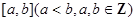 内,则
内,则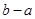 的最小值为( )
的最小值为( )
A.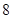 | B.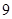 | C.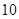 | D.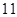 |
设 是定义在R上的奇函数,且
是定义在R上的奇函数,且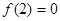 ,当
,当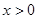 时,有
时,有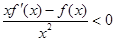 恒成立,则不等式
恒成立,则不等式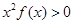 的解集是( )
的解集是( )
| A.(-2,0) ∪(2,+∞) | B.(-2,0) ∪(0,2) |
| C.(-∞,-2)∪(2,+∞) | D.(-∞,-2)∪(0,2) |
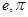 分别是自然对数的底和圆周率,则下列不等式不成立的是( )
分别是自然对数的底和圆周率,则下列不等式不成立的是( )
A.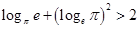 | B.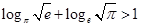 |
C.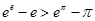 | D.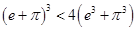 |
若曲线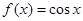 与曲线
与曲线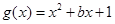 在交点
在交点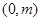 处有公切线,则
处有公切线,则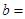 ( )
( )
A. | B. | C.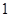 | D.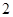 |
已知函数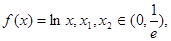 且
且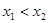 则下列结论正确的是( )
则下列结论正确的是( )
A.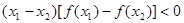 | B.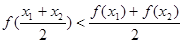 |
C.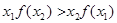 | D.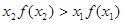 |
设函数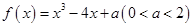 有三个零点
有三个零点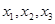 ,且
,且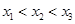 则下列结论正确的是( )
则下列结论正确的是( )
A.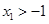 | B.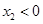 | C.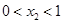 | D.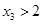 |
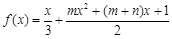 的两个极值点分别为
的两个极值点分别为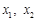 ,且
,且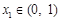 ,
,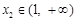 ,点
,点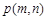 表示的平面区域为
表示的平面区域为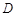 ,若函数
,若函数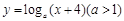 的图像上存在区域
的图像上存在区域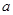 的取值范围是( )
的取值范围是( )