题目内容
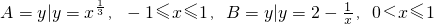 ,则A∩B=
,则A∩B=
- A.(-∞,1]
- B.[-1,1]
- C.∅
- D.{1}
B
分析:根据函数的单调性,分析可得两个函数的值域,即集合A、B,进而由交集的意义,可得答案.
解答:根据题意,分析可得,y= ,在[-1,1]上是单调增函数,故有-1≤y≤1,即A={y|-1≤y≤1},
,在[-1,1]上是单调增函数,故有-1≤y≤1,即A={y|-1≤y≤1},
y=2- 在(0,1]上是增函数,故有-2<y≤1,即B={y|-2<y≤1},
在(0,1]上是增函数,故有-2<y≤1,即B={y|-2<y≤1},
由交集的意义,可得A∩B={x|-1≤x≤1},
故选B.
点评:本题考查交集运算时与函数的值域相结合,注意结合函数的性质,求出其值域,进而求解得到答案.
分析:根据函数的单调性,分析可得两个函数的值域,即集合A、B,进而由交集的意义,可得答案.
解答:根据题意,分析可得,y=
 ,在[-1,1]上是单调增函数,故有-1≤y≤1,即A={y|-1≤y≤1},
,在[-1,1]上是单调增函数,故有-1≤y≤1,即A={y|-1≤y≤1},y=2-
 在(0,1]上是增函数,故有-2<y≤1,即B={y|-2<y≤1},
在(0,1]上是增函数,故有-2<y≤1,即B={y|-2<y≤1},由交集的意义,可得A∩B={x|-1≤x≤1},
故选B.
点评:本题考查交集运算时与函数的值域相结合,注意结合函数的性质,求出其值域,进而求解得到答案.

练习册系列答案
 期末100分闯关海淀考王系列答案
期末100分闯关海淀考王系列答案 小学能力测试卷系列答案
小学能力测试卷系列答案
相关题目
下列命题中:
①若a与b互为相反向量,则a+b=0;
②若k为实数,且k•a=0,则a=0或k=0;
③若a•b=0,则a=0或b=0;
④若a与b为平行的向量,则a•b=|a||b|;
⑤若|a|=1,则a=±1.
其中假命题的个数为( )
①若a与b互为相反向量,则a+b=0;
②若k为实数,且k•a=0,则a=0或k=0;
③若a•b=0,则a=0或b=0;
④若a与b为平行的向量,则a•b=|a||b|;
⑤若|a|=1,则a=±1.
其中假命题的个数为( )
| A、5个 | B、4个 | C、3个 | D、2个 |
命题“若a,b都是奇数,则a+b是偶数”的逆否命题是( )
| A、若a,b都不是奇数,则a+b是偶数 | B、若a+b是偶数,则a,b都是奇数 | C、若a+b不是偶数,则a,b都不是奇数 | D、若a+b不是偶数,则a,b不都是奇数 |