题目内容
下列命题中:
①若a与b互为相反向量,则a+b=0;
②若k为实数,且k•a=0,则a=0或k=0;
③若a•b=0,则a=0或b=0;
④若a与b为平行的向量,则a•b=|a||b|;
⑤若|a|=1,则a=±1.
其中假命题的个数为( )
①若a与b互为相反向量,则a+b=0;
②若k为实数,且k•a=0,则a=0或k=0;
③若a•b=0,则a=0或b=0;
④若a与b为平行的向量,则a•b=|a||b|;
⑤若|a|=1,则a=±1.
其中假命题的个数为( )
| A、5个 | B、4个 | C、3个 | D、2个 |
分析:利用相反的向量的定义及向量数乘的意义知,①②为真命题,由两个向量的数量积的定义和公式及单位向量的定义可得 ③④⑤是假命题.
解答:解:①是真命题,若
与
互为相反向量,则
=-
,∴
+
=
.
②由k为实数 且k•
=
,则得 k=0 或
=
,故②是真命题.
③不正确,由两个向量的数量积等于0,能得到这两个向量垂直,或其中一个向量为
.
④∵
•
=|
|•|
|cos<
,
,∴当
与
为平行向量时,
•
=±|
|•|
|,故④是假命题.
⑤若|
|=1,则
是单位向量,有无数个,故
=±1 是错误的,此命题是假命题.
综上,③④⑤是假命题,
故选 C.
| a |
| b |
| a |
| b |
| a |
| b |
| 0 |
②由k为实数 且k•
| a |
| 0 |
| a |
| 0 |
③不正确,由两个向量的数量积等于0,能得到这两个向量垂直,或其中一个向量为
| 0 |
④∵
| a |
| b |
| a |
| b |
| a |
| b> |
| a |
| b |
| a |
| b |
| a |
| b |
⑤若|
| a |
| a |
| a |
综上,③④⑤是假命题,
故选 C.
点评:本题考查相反的向量的定义及向量数乘的意义,两个向量的数量积的定义和公式及单位向量的定义.

练习册系列答案
相关题目
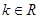 ,且
,且 ,则
,则
 ,则
,则 或
或
 ,满足|
,满足| |
| |
| |,则
|,则
 |
|