题目内容
设V是已知平面M上所有向量的集合,对于映射f:V→V,a∈V,记a的象为f(a).若映射f:V→V满足:对所有a、b∈V及任意实数λ,μ都有f(λa+μb)=λf(a)+μf(b),则f称为平面M上的线性变换.下列命题中假命题是( )
分析:对所有a、b∈V及任意实数λ,μ都有f(λa+μb)=λf(a)+μf(b),则f称为平面M上的线性变换,依题意,对A,B、C、D四个选项逐一分析即可.
解答:解:A:令λ=μ=1,则f(a+b)=f(a)+f(b),故A是真命题;
同理,D:令λ=k,μ=0,则f(ka)=kf(a),故D是真命题;
B:∵f(a)=-a,则有f(b)=-b,
f(λa+μb)=-(λa+μb)=λ•(-a)+μ(-b)=λf(a)+μf(b)是线性变换,故B是真命题;
C:由f(a)=a+
,则有f(b)=b+
,
f(λa+μb)=(λa+μb)+
=λ•(a+
)+μ•(b+
)-e=λf(a)+μf(b)-
,
∵
是单位向量,
≠0,故C是假命题.
故选:C.
同理,D:令λ=k,μ=0,则f(ka)=kf(a),故D是真命题;
B:∵f(a)=-a,则有f(b)=-b,
f(λa+μb)=-(λa+μb)=λ•(-a)+μ(-b)=λf(a)+μf(b)是线性变换,故B是真命题;
C:由f(a)=a+
| e |
| e |
f(λa+μb)=(λa+μb)+
| e |
| e |
| e |
| e |
∵
| e |
| e |
故选:C.
点评:本题考查命题的真假判断与应用,着重考查对新定义“平面M上的线性变换”的理解与应用,考查赋值法,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,记
,记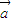 的象为
的象为 .若映射f:V→V满足:对所有
.若映射f:V→V满足:对所有 及任意实数λ,μ都有
及任意实数λ,μ都有 ,则f称为平面M上的线性变换.现有下列命题:
,则f称为平面M上的线性变换.现有下列命题:
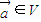 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; 是平面M上的单位向量,对
是平面M上的单位向量,对 设
设 ,则f是平面M上的线性变换;
,则f是平面M上的线性变换; ,若
,若 共线,则
共线,则 也共线.
也共线.