题目内容
 ,设
,设 (Ⅰ)求函数
(Ⅰ)求函数 的周期及单调增区间。
的周期及单调增区间。 (Ⅱ)设
 的内角
的内角 的对边分别为
的对边分别为 ,已知
,已知
 ,求边
,求边 的值.
的值.单调递增区间是[2k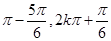 ],周期T=2
],周期T=2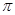 ;(Ⅱ)
;(Ⅱ)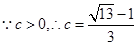
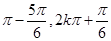 ],周期T=2
],周期T=2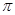 ;(Ⅱ)
;(Ⅱ)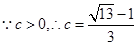
此题考查了正弦、余弦定理,三角函数的周期性及其求法,以及三角函数的恒等变换应用,涉及的知识有:两角和与差的正弦函数公式,二倍角的余弦函数公式,正弦函数的单调性,同角三角函数间的基本关系,以及三角形的边角关系,熟练掌握定理及公式是解本题的关键。
(1)(1)由两向量的坐标,利用平面向量的数量积运算法则列出关系式,再利用两角和与差的直正弦函数公式及二倍角的余弦函数公式化简,整理后得到一个角的正弦函数,找出ω的值,代入周期公式,即可求出函数的最小正周期;根据正弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到函数的递减区间;
(2)由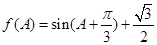
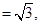 ,
,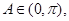 得
得 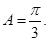
由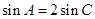 得
得 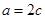 .又
.又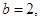 结合余弦定理得到结论。
结合余弦定理得到结论。
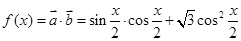
=
=

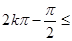 x+
x+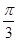
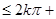
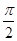 ……即2k
……即2k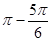
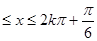 ……
……
所以…函数的单调递增区间是[2k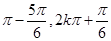 ],
],
周期T=2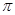 6分
6分
(Ⅱ)由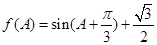
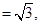 ,
,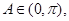 得
得 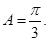
由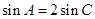 得
得 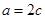 .又
.又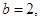
由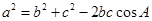 得
得 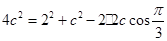
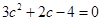 ,
,
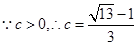 …………………………12分
…………………………12分
(1)(1)由两向量的坐标,利用平面向量的数量积运算法则列出关系式,再利用两角和与差的直正弦函数公式及二倍角的余弦函数公式化简,整理后得到一个角的正弦函数,找出ω的值,代入周期公式,即可求出函数的最小正周期;根据正弦函数的单调递减区间列出关于x的不等式,求出不等式的解集即可得到函数的递减区间;
(2)由
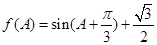
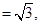 ,
,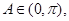 得
得 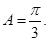
由
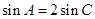 得
得 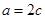 .又
.又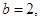 结合余弦定理得到结论。
结合余弦定理得到结论。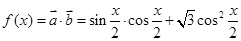
=

=


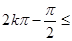 x+
x+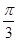
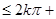
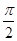 ……即2k
……即2k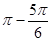
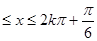 ……
……所以…函数的单调递增区间是[2k
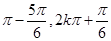 ],
],周期T=2
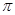 6分
6分(Ⅱ)由
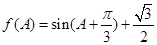
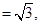 ,
,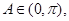 得
得 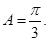
由
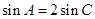 得
得 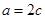 .又
.又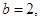
由
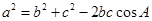 得
得 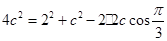
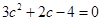 ,
, 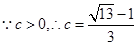 …………………………12分
…………………………12分
练习册系列答案
 期末复习检测系列答案
期末复习检测系列答案 超能学典单元期中期末专题冲刺100分系列答案
超能学典单元期中期末专题冲刺100分系列答案 黄冈360度定制密卷系列答案
黄冈360度定制密卷系列答案 阳光考场单元测试卷系列答案
阳光考场单元测试卷系列答案
相关题目
 在一个周期内的图象如图所示.则
在一个周期内的图象如图所示.则 的图象可由函数y=cosx的图象(纵坐标不变) ( )
的图象可由函数y=cosx的图象(纵坐标不变) ( )
 倍,再向左平移
倍,再向左平移 个单位
个单位 倍,再向右平移
倍,再向右平移 个单位
个单位 个单位
个单位 个单位
个单位 .
. 的最小正周期;
的最小正周期; 个单位,得到函数
个单位,得到函数 的图象,求函数
的图象,求函数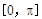 上的最大值和最小值.
上的最大值和最小值.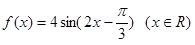 ,有下列命题:
,有下列命题: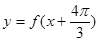 为偶函数,
为偶函数,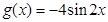 的图像,只需将
的图像,只需将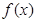 的图像向右平移
的图像向右平移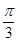 个单位,
个单位,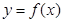 的图像关于直线
的图像关于直线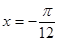 对称.
对称.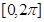 内的增区间为
内的增区间为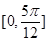 和
和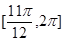 ;
;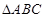 中,角
中,角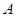 ,
,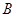 ,
,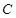 的对边分别为
的对边分别为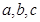 ,且
,且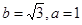 ,求
,求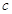 的值;(2)求sinA+sinC的最大值.
的值;(2)求sinA+sinC的最大值.  的图象,只需要把函数
的图象,只需要把函数 的图象上所有的点 ( )
的图象上所有的点 ( )

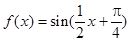 ,求函数在区间
,求函数在区间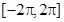 上的单调增区间;
上的单调增区间;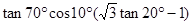 .
. 的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动
的图象上所有点的横坐标伸长到原来的2倍(纵坐标不变),再向右平行移动 单位长度,所得图象的函数解析式是( )
单位长度,所得图象的函数解析式是( )



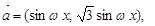
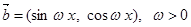
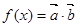 ,
,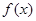 的最小正周期为
的最小正周期为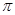 .
. 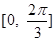 上的取值范围.
上的取值范围.