题目内容
若(x+1)4(x+4)8=a0(x+3)12+ a1(x+3)11+ a2(x+3)10+…+ a11(x+3)+a12,则log2(a1+a3+a5+…+a11)=( ).
| A.27 | B.28 | C.8 | D.7 |
D
令x="-2," 则a0+ a1+ a2+…+ a11+a12=28,
令x="-4," 则a0-a1+ a2-…-a11+a12=0,
则a0-a1+ a2-…-a11+a12=0,
两式相加得2(a1+a3+a5+…+a11)= 28,a1+a3+a5+…+a11= 27.故选D.
令x="-4,"
 则a0-a1+ a2-…-a11+a12=0,
则a0-a1+ a2-…-a11+a12=0,两式相加得2(a1+a3+a5+…+a11)= 28,a1+a3+a5+…+a11= 27.故选D.

练习册系列答案
相关题目
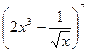 的展开式中常数项是( )
的展开式中常数项是( )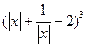 展开式中的常数项。
展开式中的常数项。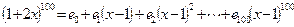 ,
,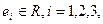 ……,
……,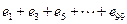 .
.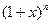 的展开式中,存在着系数之比为5:7的相邻两项,则指数
的展开式中,存在着系数之比为5:7的相邻两项,则指数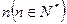 的最小值为 。
的最小值为 。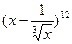 展开式中的常数项为
展开式中的常数项为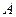 .
.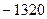
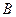 .
.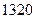
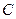 .
.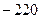
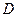 .
.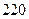
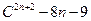 能被
能被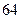 整除
整除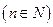 .
. ,且
,且 ,则
,则 等于( )
等于( )