题目内容
如图, 是边长为
是边长为 的正方形,点
的正方形,点 ,
, 分别为边
分别为边 ,
, 的中点,将
的中点,将 ,
, ,
, 分别沿
分别沿 ,
, ,
, 折起,使
折起,使 三点重合于点
三点重合于点 ,若四面体
,若四面体 的四个顶点在同一个球面上,则该球的表面积是( )
的四个顶点在同一个球面上,则该球的表面积是( )

A.  B.
B. 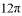 C.
C.  D.
D. 
练习册系列答案
相关题目
题目内容
如图, 是边长为
是边长为 的正方形,点
的正方形,点 ,
, 分别为边
分别为边 ,
, 的中点,将
的中点,将 ,
, ,
, 分别沿
分别沿 ,
, ,
, 折起,使
折起,使 三点重合于点
三点重合于点 ,若四面体
,若四面体 的四个顶点在同一个球面上,则该球的表面积是( )
的四个顶点在同一个球面上,则该球的表面积是( )

A.  B.
B. 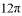 C.
C.  D.
D. 