题目内容

已知直线的参数方程为，（t为参数），以坐标原点为极点，x轴的正半轴为极轴建立极坐标系，圆C的极坐标方程为.
（1）把圆C的极坐标方程化为直角坐标方程；
（2）将直线向右平移h个单位，所得直线与圆C相切，求h.

（1）；（2）或.

解析试题分析：本题考查直角坐标系与极坐标系之间的互化、参数的几何意义、函数图像的平移等基础知识，考查学生的转化能力和计算能力.第一问，利用极坐标方程与直角坐标方程的互化公式，可将圆C化为直角坐标方程；第二问，直接将直线的参数方程进行平移，消参，由于直线与圆相切，所以消参后的方程的判别式等于0，解出h的值.
试题解析：（1）因为，，所以圆C的直角坐标方程为
．      4分
（2）平移直线后，所得直线l¢的（t为参数）．
．
因为与圆相切，所以
，即，
解得或．       10分
考点：1.极坐标方程与直角坐标方程的互化；2.参数方程；3.图像平移.

练习册系列答案
相关题目

在极坐标系中，曲线的极坐标方程为，现以极点为原点，极轴为轴的非负半轴建立平面直角坐标系，直线的参数方程为（为参数）
（1）写出直线l和曲线C的普通方程；
（2）设直线l和曲线C交于A，B两点，定点P（—2，—3），求|PA|·|PB|的值．

在极坐标系中，已知曲线C1：ρ＝12sinθ，曲线C2：ρ＝12cos.
(1)求曲线C1和C2的直角坐标方程；
(2)若P、Q分别是曲线C1和C2上的动点，求PQ的最大值．

已知直线的参数方程为为参数)，以坐标原点为极点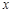，轴的正半轴为极轴建立极坐标系，圆的极坐标方程为．
（1）求圆的直角坐标方程；
（2）若是直线与圆面≤的公共点，求的取值范围．

已知曲线C的极坐标方程为ρ2=,以极点为原点,极轴所在直线为x轴建立平面直角坐标系.
(1)求曲线C的直角坐标方程及参数方程.
(2)若P(x,y)是曲线C上的一个动点,求x+2y的最小值,并求P点的坐标.

将下列各极坐标方程化为直角坐标方程.
(1)θ=(ρ∈R).　(2)ρcos2=1.

在直角坐标系xOy中,以O为极点,x轴非负半轴为极轴建立极坐标系,曲线C的极坐标方程为ρcos(θ-)=1,M,N分别为C与x轴,y轴的交点.
(1)写出C的直角坐标方程,并求M,N的极坐标.
(2)设MN的中点为P,求直线OP的极坐标方程.

求圆被直线(是参数)截得的弦长．

在极坐标系中，圆C的方程为ρ＝2 sin ，以极点为坐标原点，极轴为x轴的正半轴建立平面直角坐标系，直线l的参数方程为 (t为参数)，判断直线l和圆C的位置关系．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网