题目内容
设集合A={1，2，3，4}，B={x|x2-a=0，x∈N}，若满足B⊆A，求实数a的集合．
解：因为集合B中，x∈N，则由x2-a=0，得x2=a，所以a≥0，所以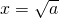
，
因为B⊆A，所以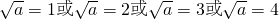
，
解得a=1或a=4或a=9或a=16．
即a的集合为{1，4，9，16}．
分析：先确定集合B中方程的解，然后根据集合关系确定集合元素的关系．
点评：本题主要考查集合关系的应用，利用集合关系确定元素的关系是解决本题的关键．
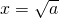，因为B⊆A，所以
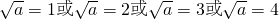，解得a=1或a=4或a=9或a=16．
即a的集合为{1，4，9，16}．
分析：先确定集合B中方程的解，然后根据集合关系确定集合元素的关系．
点评：本题主要考查集合关系的应用，利用集合关系确定元素的关系是解决本题的关键．
练习册系列答案
备战中考寒假系列答案
相关题目