题目内容
某几何体的三视图如图所示,它的全面积为 ．、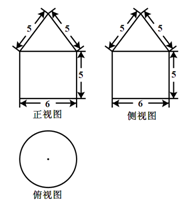
解析试题分析：根据题意可知该几何体是圆锥和圆柱的组合体，圆柱底面半径为3，高为5，圆锥的高为4，那么可知全面积为S=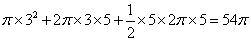
,故答案为
考点：三视图
点评：本题考查由三视图求面积，考查计算能力，是基础题．
练习册系列答案
智慧小复习系列答案
相关题目
智慧小复习系列答案题目内容
某几何体的三视图如图所示,它的全面积为 ．、
解析试题分析：根据题意可知该几何体是圆锥和圆柱的组合体，圆柱底面半径为3，高为5，圆锥的高为4，那么可知全面积为S=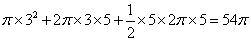 ,故答案为
考点：三视图
点评：本题考查由三视图求面积，考查计算能力，是基础题．
智慧小复习系列答案
和直线
，
所围成的平面图形，绕
轴旋转一周所得到的旋转体为
；由同时满足
，
，
，
的点
构成的平面图形,绕
.根据祖暅原理等知识，通过考察
的正方形，其中一个的某顶点在另一个的中心，则这两个正方形重叠部分的面积恒为
．类比到空间，有两个棱长均为
、
、
的面积分别为
、
、
，则三棱锥A-BCD的外接球的体积为_______．
的棱长为1，
分别为线段
上的点，则三棱锥
的体积为____________.
, 则正方体的棱长为 .