题目内容
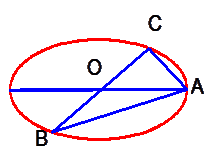
已知![]() 是长轴为4的椭圆上的三点,点
是长轴为4的椭圆上的三点,点![]() 是长轴的一个顶点,
是长轴的一个顶点,![]() 过椭圆中心
过椭圆中心![]() (如图),且
(如图),且![]() ,
,![]()
(I)求椭圆的方程;
 (Ⅱ)如果椭圆上的两点
(Ⅱ)如果椭圆上的两点![]() ,使
,使![]() 的平分线垂直于
的平分线垂直于![]() ,是否总存在实数
,是否总存在实数![]() ,使
,使![]() 。请给出证明。
。请给出证明。
)
由条件,设所求的椭圆方程为![]() 其 中
其 中 ![]()
![]()
![]() ,
,![]() 则
则![]() ,且
,且![]()
![]() 代入椭圆方程得
代入椭圆方程得![]()
即椭圆方程为![]()
(Ⅱ)若![]() 的平分线垂直于
的平分线垂直于![]() ,则
,则![]() 倾斜角互补,设
倾斜角互补,设![]() 所在的直线方程为
所在的直线方程为![]() 由方程组
由方程组
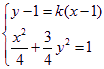 可得
可得 ![]()
![]() 且
且![]() ,代入
,代入![]() 中可得
中可得![]()
同理可得
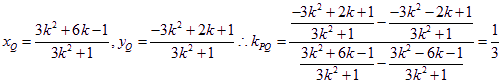
又![]() 总存在
总存在![]() 使
使![]()
解析:

练习册系列答案
相关题目
 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且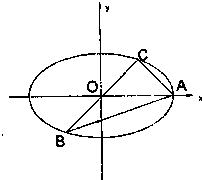 如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且
如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的右顶点,BC过椭圆中心O,且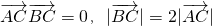 ,
,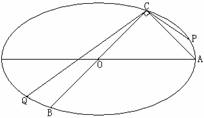 (满分14分)如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且满足
(满分14分)如图,已知A、B、C是长轴为4的椭圆上的三点,点A是长轴的一个端点,BC过椭圆中心O,且满足