题目内容
对于x∈R,函数f(x)满足f(1-x)=f(1+x),f(x+2)=f(x),若当x∈(0,1]时,f(x)=x+1,则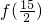 等于
等于
- A.

- B.

- C.

- D.

B
分析:由f(x+2)=f(x),得到函数的周期是2,由f(1-x)=f(1+x),得到函数关于x=1对称,然后利用周期和对称将 转化到(0,1)内的数值进行求解.
转化到(0,1)内的数值进行求解.
解答:因为f(x+2)=f(x),所以函数的周期是2.又f(1-x)=f(1+x),所以函数关于x=1对称,
所以f( )=f(2×
)=f(2× )=f(
)=f( )=f(1+
)=f(1+ )=f(1-
)=f(1- )=f(
)=f( ),
),
因为x∈(0,1]时,f(x)=x+1,所以f( )=
)=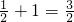 ,
,
故选B.
点评:本题考查了函数的周期性和对称性的应用,要求熟练掌握函数性质的综合应用.
分析:由f(x+2)=f(x),得到函数的周期是2,由f(1-x)=f(1+x),得到函数关于x=1对称,然后利用周期和对称将
 转化到(0,1)内的数值进行求解.
转化到(0,1)内的数值进行求解.解答:因为f(x+2)=f(x),所以函数的周期是2.又f(1-x)=f(1+x),所以函数关于x=1对称,
所以f(
 )=f(2×
)=f(2× )=f(
)=f( )=f(1+
)=f(1+ )=f(1-
)=f(1- )=f(
)=f( ),
),因为x∈(0,1]时,f(x)=x+1,所以f(
 )=
)=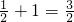 ,
,故选B.
点评:本题考查了函数的周期性和对称性的应用,要求熟练掌握函数性质的综合应用.

练习册系列答案
 口算题天天练系列答案
口算题天天练系列答案
相关题目