题目内容
对于x∈R,函数f(x)表示x-1与|x2-4x+3|中大的一个值.(1)求f(0),f(1),f(2),f(3);
(2)作出y=f(x)的图象;
(3)在[0,2]内,求f(x)的值域.
【答案】分析:(1)由函数f(x)表示x-1与|x2-4x+3|中大的一个值,将0,1,2,3分别代入可得答案.
(2)利用零点分段法,结合二次函数的图象和性质,求出y=f(x)的解析式,并将其写成分段函数的形式,进而根据分段函数的图象分段画的原则,可得函数y=f(x)的图象;
(3)由(2)中函数的图象,分析x∈[0,2]时,函数值的取值范围,可得f(x)的值域.
解答:解:(1)当x=0时,x-1=-1,|x2-4x+3|=3,故f(0)=3,
当x=1时,x-1=0,|x2-4x+3|=0,故f(1)=0,
当x=2时,x-1=1,|x2-4x+3|=-1,故f(2)=1,
当x=3时,x-1=2,|x2-4x+3|=0,故f(3)=2.
(2)y=f(x)=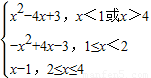 ,
,
其图象如下图所示:
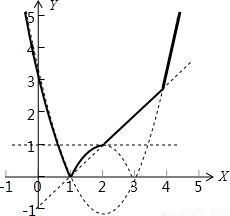
(3)由图象可得:
当x∈[0,2]时,f(x)∈[0,3]
即f(x)的值域为[0,3]
点评:本题考查的知识点是函数的值域,函数图象的作法,函数的值,熟练掌握二次函数的图象和性质,及函数图象的对折变换是解答的关键.
(2)利用零点分段法,结合二次函数的图象和性质,求出y=f(x)的解析式,并将其写成分段函数的形式,进而根据分段函数的图象分段画的原则,可得函数y=f(x)的图象;
(3)由(2)中函数的图象,分析x∈[0,2]时,函数值的取值范围,可得f(x)的值域.
解答:解:(1)当x=0时,x-1=-1,|x2-4x+3|=3,故f(0)=3,
当x=1时,x-1=0,|x2-4x+3|=0,故f(1)=0,
当x=2时,x-1=1,|x2-4x+3|=-1,故f(2)=1,
当x=3时,x-1=2,|x2-4x+3|=0,故f(3)=2.
(2)y=f(x)=
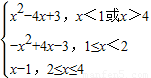 ,
,其图象如下图所示:

(3)由图象可得:
当x∈[0,2]时,f(x)∈[0,3]
即f(x)的值域为[0,3]
点评:本题考查的知识点是函数的值域,函数图象的作法,函数的值,熟练掌握二次函数的图象和性质,及函数图象的对折变换是解答的关键.

练习册系列答案
相关题目