题目内容
有下列四个命题:
①对于?x∈R,函数f(x)满足f(1+x)=f(1-x),则函数f(x)的最小正周期为2;
②所有指数函数的图象都经过点(0,1);
③若实数a,b满足a+b=1,则
+
的最小值为9;
④已知两个非零向量
,
,则“
⊥
”是“
•
=0”的充要条件.
其中真命题的个数为( )
①对于?x∈R,函数f(x)满足f(1+x)=f(1-x),则函数f(x)的最小正周期为2;
②所有指数函数的图象都经过点(0,1);
③若实数a,b满足a+b=1,则
| 1 |
| a |
| 4 |
| b |
④已知两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
其中真命题的个数为( )
分析:①利用函数的周期性和对称性判断.②利用指数函数的性质判断.③利用基本不等式证明.④利用向量垂直的充要条件判断.
解答:解:①满足f(1+x)=f(1-x),则函数关于x=1对称,所以①错误.
②因为a0=1,所以所有指数函数的图象都经过点(0,1),所以②正确.
③
+
=(
+
)(a+b)=1+4+
+
≥5+2
=9,当且仅当
=
,即b=2a=
时取等号,所以③正确.
④因为两个非零向量
,
,所以“
⊥
”是“
•
=0”的充要条件,所以④正确.
故选C.
②因为a0=1,所以所有指数函数的图象都经过点(0,1),所以②正确.
③
| 1 |
| a |
| 4 |
| b |
| 1 |
| a |
| 4 |
| b |
| b |
| a |
| 4a |
| b |
|
| b |
| a |
| 4a |
| b |
| 1 |
| 2 |
④因为两个非零向量
| a |
| b |
| a |
| b |
| a |
| b |
故选C.
点评:本题主要考查命题的真假判断,涉及的知识点较多,综合性较强.

练习册系列答案
相关题目
 B
B 对任意x∈A都有x
对任意x∈A都有x B;②A
B;②A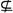 B
B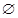 ; ③A
; ③A