题目内容
【题目】已知数列![]() ,
,![]() ,其前
,其前![]() 项和
项和![]() 满足
满足![]() ,其中
,其中![]() .
.
(1)设![]() ,证明:数列
,证明:数列![]() 是等差数列;
是等差数列;
(2)设![]() ,
,![]() 为数列
为数列![]() 的前
的前![]() 项和,求证:
项和,求证:![]() ;
;
(3)设![]() (
(![]() 为非零整数,
为非零整数,![]() ),试确定
),试确定![]() 的值,使得对任意
的值,使得对任意![]() ,都有
,都有![]() 成立.
成立.
【答案】(1)证明见解析;(2)证明见解析;(3)![]() .
.
【解析】
试题分析:(1)当![]() 时,得到
时,得到![]() ,当
,当![]() 时,
时,![]() ,即可化简
,即可化简![]() ,即可证得结论;(2)由(1)可得
,即可证得结论;(2)由(1)可得![]()
![]() ,利用乘公比错误相减法,即可求解数列的和;(3)由
,利用乘公比错误相减法,即可求解数列的和;(3)由![]() 得
得![]() ,整理得
,整理得![]() ,当
,当![]() 为奇数时,
为奇数时,![]() ,∴
,∴![]() ;当
;当![]() 为偶数时,
为偶数时,![]() ,∴
,∴![]() ,由
,由![]() 为非零整数,即可求解
为非零整数,即可求解![]() .
.
试题解析:(1)当![]() 时,
时,![]() ,∴
,∴![]() ,
,
当![]() 时,
时,![]() ,
,
∴![]() ,即
,即![]() ,∴
,∴![]() (常数),
(常数),
又![]() ,∴
,∴![]() 是首项为2,公差为1的等差数列,∴
是首项为2,公差为1的等差数列,∴![]() .
.
(2)![]()
![]() ,
,
∴![]() ,
,
![]() ,
,
相减得![]()
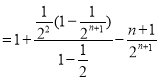
![]() ,
,
∴![]() .
.
(3)由![]() ,得
,得![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
当![]() 为奇数时,
为奇数时,![]() ,∴
,∴![]() ;
;
当![]() 为偶数时,
为偶数时,![]() ,∴
,∴![]() ,
,
∴![]() ,又
,又![]() 为非零整数,∴
为非零整数,∴![]() .
.

练习册系列答案
相关题目
【题目】已知函数![]() 的定义域
的定义域![]() ,部分对应值如表,
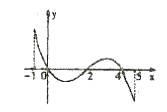
,部分对应值如表, ![]() 的导函数
的导函数![]() 的图象如图所示,下列关于函数
的图象如图所示,下列关于函数![]() 的命题;
的命题;
|
|
|
|
|
|
|
|
|
|
|
|
①函数![]() 的值域为
的值域为![]() ;
;
②函数![]() 在
在![]() 上是减函数;
上是减函数;
③如果当![]() 时,
时, ![]() 最大值是
最大值是![]() ,那么
,那么![]() 的最大值为
的最大值为![]() ;
;
④当![]() 时,函数
时,函数![]() 最多有4个零点.
最多有4个零点.
其中正确命题的序号是_________.