题目内容

已知存在实数x使得不等式|x-3|-|x+2|≥|3a-1|成立，则实数a的取值范围是
 
．
分析：由题意知这是一个存在性的问题，须求出不等式左边的最大值，令其大于等于|3a-1|，即可解出实数a的取值范围
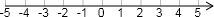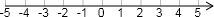解答：精英家教网解：由题意借助数轴，|x-3|-|x+2|∈[-5，5]
∵存在实数x使得不等式|x-3|-|x+2|≥|3a-1|成立，
∴5≥|3a-1|，解得-5≤3a-1≤5，即-
4
3
≤a≤2
故答案为[-
4
3
，2]
点评：本题考查绝对值不等式，求解本题的关键是正确理解题意，区分存在问题与恒成立问题的区别，本题是一个存在问题，解决的是有的问题，故取|3a-1|≤5，即小于等于左边的最大值即满足题意，本题是一个易错题，主要错误就是出在把存在问题当成恒成立问题求解，因思维错误导致错误．
练习册系列答案
相关题目
下列命题中：
①函数f(x)=x+
2
x
(x∈(0，1))的最小值是2
2
；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x）且x＞0时，f′（x）＞0，g′（x）＞0，则x＜0时，f′（x）＞g′（x）；
③如果y=f（x）是可导函数，则f′（x0）=0是函数y=f（x）在x=x0处取到极值的必要不充分条件；
④已知存在实数x使得不等式|x+1|-|x-1|≤a成立，则实数a的取值范围是a≥2．
其中正确的命题是
②③
②③
．
已知函数f（x）=
46+x-x2
，g（x）=x2-3ax+2a2（a＜0），若不存在实数x使得f（x）＞1和g（x）＜0同时成立，试求a的范围．
已知函数 f(x)=
4
6+x-x2
，g(x)=|x-
(a+1)2
2
|，若不存在实数x使得f(x)＞1和g(x)≤
(a-1)2
2
同时成立，试求 a的取值范围．
下列命题中：
①函数f(x)=x+
2
x
(x∈(0，1))的最小值是2
2
；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x）且x＞0时，f′（x）＞0，g′（x）＞0，则x＜0时，f′（x）＞g′（x）；
③如果y=f（x）是可导函数，则f′（x0）=0是函数y=f（x）在x=x0处取到极值的必要不充分条件；
④已知存在实数x使得不等式|x+1|-|x-1|≤a成立，则实数a的取值范围是a≥2．
其中正确的命题是______．
下列命题中：
①函数的最小值是；
②对于任意实数x，有f（-x）=-f（x），g（-x）=g（x）且x＞0时，f′（x）＞0，g′（x）＞0，则x＜0时，f′（x）＞g′（x）；
③如果y=f（x）是可导函数，则f′（x）=0是函数y=f（x）在x=x处取到极值的必要不充分条件；
④已知存在实数x使得不等式|x+1|-|x-1|≤a成立，则实数a的取值范围是a≥2．
其中正确的命题是    ．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网