题目内容
已知圆C:x2+y2=r2(r>0)经过点(1,).
(1)求圆C的方程;
(2)是否存在经过点(-1,1)的直线l,它与圆C相交于A,B两个不同点,且满足=+(O为坐标原点)关系的点M也在圆C上?如果存在,求出直线l的方程;如果不存在,请说明理由.
(1)由圆C:x2+y2=r2,再由点(1,)在圆C上,得r2=12+()2=4
所以圆C的方程为
x2+y2=4;
(2)假设直线l存在,
设A(x1,y1),B(x2,y2),
M(x0,y0)
①若直线l的斜率存在,设直线l的方程为:
y-1=k(x+1),
联立
消去y得,
(1+k2)x2+2k(k+1)x+k2+2k-3=0,
由韦达定理得x1+x2
=-=-2+,
x1x2==1+,
y1y2=k2x1x2+k(k+1)(x1+x2)+(k+1)2=-3,
因为点A(x1,y1),B(x2,y2)在圆C上,
因此,得x+y=4,
x+y=4,
由=+得x0
=,y0=,
由于点M也在圆C上,
则2+2
=4,
整理得,+3+x1x2+y1y2=4,
即x1x2+y1y2=0,所以1++(-3)=0,
从而得,k2-2k+1=0,即k=1,因此,直线l的方程为
y-1=x+1,即x-y+2=0,
②若直线l的斜率不存在,
则A(-1,),B(-1,-),M
2+2
=4-≠4,
故点M不在圆上与题设矛盾
综上所知:k=1,直线方程为x-y+2=0
解析

练习册系列答案
相关题目
设 是椭圆
是椭圆 的左、右焦点,
的左、右焦点, 为直线
为直线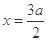 上一点,
上一点,
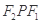 是底角为
是底角为 的等腰三角形,则
的等腰三角形,则 的离心率为( )
的离心率为( )
A. | B. | C. | D. |
已知椭圆的一个焦点为F(0,1),离心率 ,则该椭圆的标准方程为
,则该椭圆的标准方程为
A. | B. | C.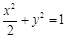 | D. |
 中O是坐标原点,
中O是坐标原点, ,圆
,圆 是
是 的外接圆,过点(2,6)的直线为
的外接圆,过点(2,6)的直线为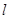 。
。 ,求直线
,求直线 =a,
=a, =b(a>2,b>2).
=b(a>2,b>2). 的圆心为
的圆心为 ,圆
,圆 :
: 的圆心为
的圆心为 的轨迹方程;
的轨迹方程;  ,使得
,使得 为钝角?若存在,求出点
为钝角?若存在,求出点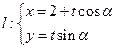 (
(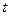 为参数),圆
为参数),圆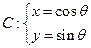 (
( 为参数).
为参数).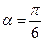 时,试判断直线
时,试判断直线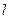 与圆
与圆 的位置关系;
的位置关系;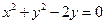 上任一点
上任一点
 的取值范围
的取值范围 恒成立,求实数C的最小值,
恒成立,求实数C的最小值, 的方程为
的方程为 ,圆
,圆 的极坐标方程为
的极坐标方程为  .
.