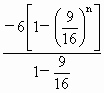题目内容
| |||||||||||
答案:
解析:
解析:
(1) |
解析:∵4(an+1-an)(an-1)+(an-1)2=0,∴(an-1)(4an+1-3an-1)=0. ∵a1=2,∴an≠1,∴4an+1=3an+1. 假设存在常数c,使{an+c}成等比数列. 则由 ∴存在常数c=-1.使{an-1}成等比数列. |
(2) |
an-1= 从而bn=3(an-1)2-[4(an+1-1)]2 =3 ∴bn=(-6)( ∴Sn=b1+b2+…+bn= =- 点评:此题综合了数列与函数的知识,又是探索性问题.其解法具有一定的代表性. |

练习册系列答案
相关题目
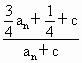 =
=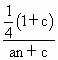 为常数.∴c=-1,
为常数.∴c=-1,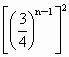 -
-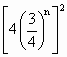 ,
,