题目内容
如图,在三棱柱A1B1C1 ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F
ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F ADE的体积为V1,三棱柱A1B1C1
ADE的体积为V1,三棱柱A1B1C1 ABC的体积为V2,则V1∶V2= .
ABC的体积为V2,则V1∶V2= . 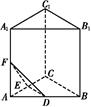
1∶24
解析

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
题目内容
如图,在三棱柱A1B1C1 ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F
ABC中,D,E,F分别是AB,AC,AA1的中点.设三棱锥F ADE的体积为V1,三棱柱A1B1C1
ADE的体积为V1,三棱柱A1B1C1 ABC的体积为V2,则V1∶V2= .
ABC的体积为V2,则V1∶V2= . 
1∶24
解析

 名校课堂系列答案
名校课堂系列答案