题目内容
(本题满分14分)
已知三条直线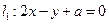
 ,直线
,直线 和直线
和直线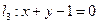 ,且
,且 与
与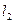 的距离是
的距离是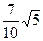
(1)求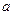 的值
的值
(2)能否找到一点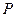 ,使得
,使得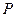 点同时满足下面三个条件,①
点同时满足下面三个条件,①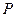 是第一象限的点;②
是第一象限的点;②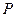 到
到 的距离是
的距离是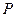 到
到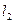 距离的
距离的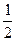 ,③
,③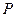 点到
点到 的距离与
的距离与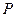 到
到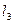 的距离之比是
的距离之比是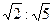 ,若能,
,若能, 求点
求点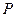 的坐标,若不能,说明理由。
的坐标,若不能,说明理由。
解:(1)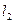 即
即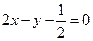 ,∴
,∴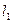 与
与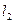 的距离
的距离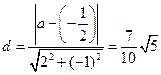
∴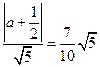 ∴
∴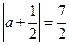 ∵
∵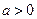 ∴
∴
(2)设点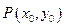 ,若
,若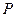 点满足条件②,则
点满足条件②,则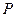 点
点 在与
在与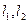 平行的直线
平行的直线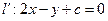 上,且
上,且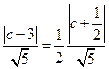 ,即
,即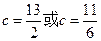 , ∴
, ∴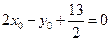 或
或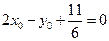
若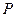 点满足条件③,由点到直线的距离公式,有
点满足条件③,由点到直线的距离公式,有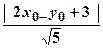 =
=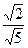 ·
·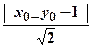 ,即
,即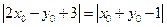

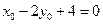 ,或3x0+2=0
,或3x0+2=0
由于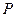 在第一象限,∴3x0+2=0不可能
在第一象限,∴3x0+2=0不可能
联立 方程
方程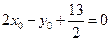 和
和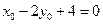 ,解得
,解得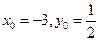 舍去,
舍去,
由 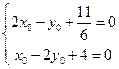 解得
解得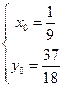
∴点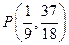 即为同时满
即为同时满 足三个条件的点
足三个条件的点
解析

练习册系列答案
相关题目
 满足圆的标准方程
满足圆的标准方程 ,
, 的最小值;
的最小值; 到圆上点的最大值.
到圆上点的最大值. 和
和 的交点且与直线
的交点且与直线 垂直的直线方程.
垂直的直线方程.
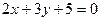 平行且距离等于
平行且距离等于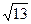 的直线
的直线 方程.
方程. 
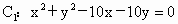 和圆
和圆 相交于A、B两点,求公共弦AB所在的直线方程,并求弦AB的长.(10)
相交于A、B两点,求公共弦AB所在的直线方程,并求弦AB的长.(10) 中,已知圆
中,已知圆 的圆心为
的圆心为 ,过点
,过点 且斜率为
且斜率为 的直线与圆
的直线与圆 .
. 与
与 共线?如果存在,求
共线?如果存在,求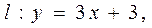
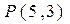 关于直线
关于直线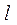 的对称点
的对称点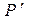 的坐标;
的坐标;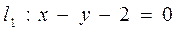 关于直线
关于直线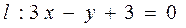 的对称直线
的对称直线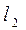 的方程。
的方程。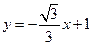 和
和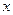 轴,
轴,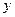 轴分别交于点
轴分别交于点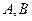 ,以线段
,以线段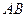 为边在第一象限内作等边△
为边在第一象限内作等边△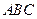 ,如果在第一象限内有一点
,如果在第一象限内有一点 使得△
使得△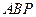 和△
和△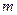 的值。
的值。