题目内容
，
为非零向量，“函数f（x）=（x+
）2为偶函数”是“
⊥”的（ ）
|
| A． | 充分但不必要条件 | B． | 必要但不充分条件 |
|
| C． | 充要条件 | D． | 既不充分也不必要条件 |
考点：
数量积判断两个平面向量的垂直关系；充要条件．
专题：
计算题．
分析：
利用向量的运算法则化简f（x）；利用向量垂直的充要条件及偶函数的定义，先判断由前者是否推出后者；由后者是否推出前者；利用充要条件的定义得到结论．
解答：
解：∵
若f（x）为偶函数，则有
则有
则有
反之，若
则有
则有
所以f（x）为偶函数
故函数
为偶函数是的充要条件
故选C
点评：
本题考查向量垂直的充要条件、考查偶函数的定义、考查如何判断一个命题是另一个命题的什么条件．
练习册系列答案
相关题目
| a |
| b |
| a |
| b |
| a |
| b |
| A、充分但不必要条件 |
| B、必要但不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知
，
为非零向量，函数f(x)=(x
+
)•(
-x
)，则使f（x）的图象为关于y轴对称的抛物线的一个必要不充分条件是（ ）
| a |
| b |
| a |
| b |
| a |
| b |
A、
| ||||
B、
| ||||
C、|
| ||||
D、
|
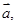
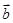为非零向量，“函数
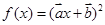为偶函数”是“
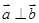”的
| A．充分但不必要条件 | B．必要但不充分条件 |
| C．充要条件 | D．既不充分也不必要条件 |
为非零向量，函数
，则使f（x）的图象为关于y轴对称的抛物线的一个必要不充分条件是（ ）
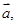
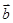为非零向量，“函数
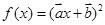为偶函数”是“
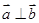”的