题目内容
如图,在组合体中,ABCD—A1B1C1D1是一个长方体,P—ABCD是一个四棱锥.AB=2,BC=3,点P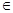 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD=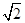 .
.
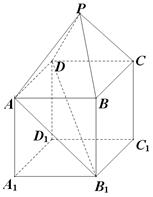
(1)证明:PD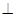 平面PBC;
平面PBC;
(2)求PA与平面ABCD所成的角的正切值;
(3)若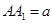 ,当a为何值时,PC//平面
,当a为何值时,PC//平面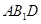 .
.
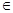 平面CC1D1D,且PC=PD=
平面CC1D1D,且PC=PD=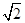 .
.
(1)证明:PD
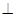 平面PBC;
平面PBC;(2)求PA与平面ABCD所成的角的正切值;
(3)若
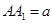 ,当a为何值时,PC//平面
,当a为何值时,PC//平面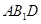 .
.(1)先证 ,再证
,再证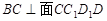 ,根据线面垂直的判定定理可证结论
,根据线面垂直的判定定理可证结论
(2) (3)当
(3)当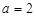 时,
时,
或建立空间直角坐标系可以用空间向量解决
 ,再证
,再证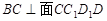 ,根据线面垂直的判定定理可证结论
,根据线面垂直的判定定理可证结论(2)
 (3)当
(3)当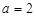 时,
时,
或建立空间直角坐标系可以用空间向量解决
试题分析:方法一:(1)因为
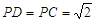 ,
,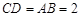 ,
,所以
 为等腰直角三角形,所以
为等腰直角三角形,所以 .
. 因为
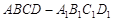 是一个长方体,所以
是一个长方体,所以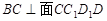 ,
,而
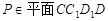 ,所以
,所以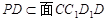 ,所以
,所以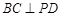 .
. 因为
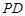 垂直于平面
垂直于平面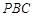 内的两条相交直线
内的两条相交直线 和
和 ,
,由线面垂直的判定定理,可得
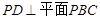 .
.
(2)过
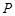 点在平面
点在平面 作
作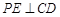 于
于 ,连接
,连接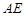 .
.因为
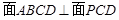 ,所以
,所以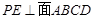 ,
,所以
 就是
就是 与平面
与平面 所成的角.
所成的角.因为
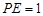 ,
, ,所以
,所以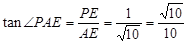 .
. 所以
 与平面
与平面 所成的角的正切值为
所成的角的正切值为 .
. (3)当
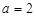 时,
时, .
. 当
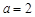 时,四边形
时,四边形 是一个正方形,所以
是一个正方形,所以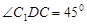 ,
,而
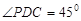 ,所以
,所以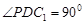 ,所以
,所以 .
. 而
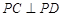 ,
,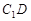 与
与 在同一个平面内,所以
在同一个平面内,所以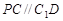 .
. 而
 ,所以
,所以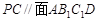 ,所以
,所以 .
.方法二:(1)证明:如图建立空间直角坐标系,设棱长
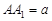 ,
,则有
 ,
, ,
, ,
, .
. 于是
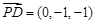 ,
,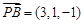 ,
, ,
,所以
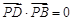 ,
,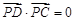 .
.所以
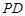 垂直于平面
垂直于平面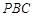 内的两条相交直线
内的两条相交直线 和
和 ,
,由线面垂直的判定定理,可得
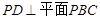 .
. 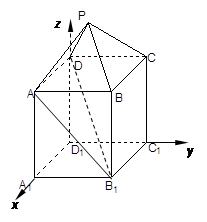
(2)解:
 ,所以
,所以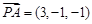 ,而平面
,而平面 的一个法向量为
的一个法向量为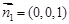 .
.所以
 .所以
.所以 与平面
与平面 所成的角的正切值为
所成的角的正切值为 .
. (3)解:
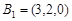 ,所以
,所以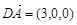 ,
,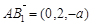 .
.设平面
 的法向量为
的法向量为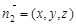 ,则有
,则有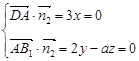 ,
,令
 ,可得平面
,可得平面 的一个法向量为
的一个法向量为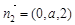 .
. 若要使得
 ,则要
,则要 ,即
,即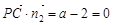 ,解得
,解得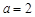 .
.所以当
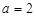 时,
时, .
.
点评:解决空间中直线、平面间的位置关系,要紧扣相应的判定定理和性质定理,求线面角时,要注意先作再证再求,要注意线面角的取值范围.

练习册系列答案
 小学期末标准试卷系列答案
小学期末标准试卷系列答案
相关题目
 中,底面ABCD是一直角梯形,
中,底面ABCD是一直角梯形, ,
, ,
, ,且PA=AD=DC=
,且PA=AD=DC= AB=1.
AB=1.
 平面
平面
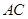 与
与 所成角的余弦值
所成角的余弦值 --
-- ,E、F分别是
,E、F分别是 、
、 的中点,p是
的中点,p是 B、线段
B、线段
 D、线段
D、线段 垂直平行四边形
垂直平行四边形 所在平面,若
所在平面,若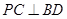 ,则平行四边形
,则平行四边形 (填形状)
(填形状)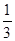 ,则侧棱与底面所成角的正弦值为( )
,则侧棱与底面所成角的正弦值为( )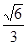
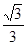
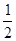
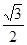
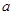 的菱形
的菱形 中,
中,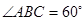 ,
,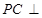 面
面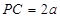 ,
,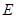 、
、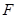 分别是
分别是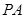 和
和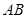 的中点.
的中点.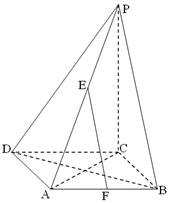
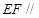 面
面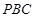 ;
; 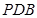 ⊥平面
⊥平面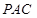 ;
;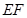 与平面
与平面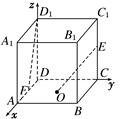
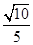
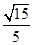
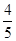
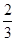
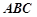 是正三角形,
是正三角形,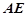 和
和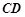 都垂直于平面
都垂直于平面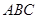 ,且
,且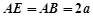 ,
,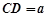 ,
,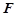 是
是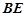 的中点.
的中点.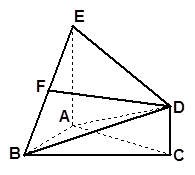
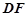 ∥平面
∥平面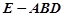 的体积.
的体积. 、β是两个不同的平面,则下列命题中正确的是
、β是两个不同的平面,则下列命题中正确的是