题目内容
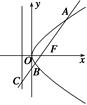
如图,过抛物线y2=2px (p>0)的焦点F的直线l交抛物线于点A、B,交其准线于点C,若|BC|=2|BF|,且|AF|=3,则此抛物线方程为( )
A.y2=9x B.y2=6x
C.y2=3x D.y2=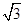 x
x

A.y2=9x B.y2=6x
C.y2=3x D.y2=
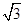 x
xC
如图,∵|BC|=2|BF|,
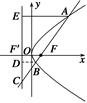
∴由抛物线的定义可知∠BCD=30°,
|AE|=|AF|=3,∴|AC|=6.
即F为AC的中点,
∴p=|FF′|=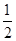 |EA|=
|EA|=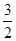 ,故抛物线方程为y2=3x.
,故抛物线方程为y2=3x.

∴由抛物线的定义可知∠BCD=30°,
|AE|=|AF|=3,∴|AC|=6.
即F为AC的中点,
∴p=|FF′|=
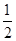 |EA|=
|EA|=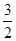 ,故抛物线方程为y2=3x.
,故抛物线方程为y2=3x.
练习册系列答案
 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
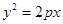 (
( )的准线与
)的准线与 轴交于点
轴交于点 .
.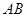 (直线与抛物线交于点
(直线与抛物线交于点 ,
, ),使得三角形
),使得三角形 的面积
的面积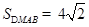 ?若存在,请求出直线
?若存在,请求出直线 ,斜率为2的直线l过点A(2,3).
,斜率为2的直线l过点A(2,3).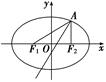
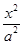 +
+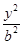 =1
=1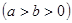 的离心率为
的离心率为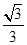 ,左焦点为F(-1,0),
,左焦点为F(-1,0),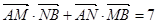 ,求直线L的方程;
,求直线L的方程;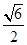 ?
? 的圆心在坐标原点O,且恰好与直线
的圆心在坐标原点O,且恰好与直线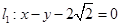 相切.
相切.
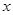 轴于N,若动点Q满足
轴于N,若动点Q满足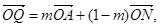 (其中m为非零常数),试求动点
(其中m为非零常数),试求动点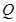 的轨迹方程
的轨迹方程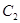 .
.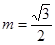 时,得到动点Q的轨迹曲线C,与
时,得到动点Q的轨迹曲线C,与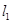 垂直的直线
垂直的直线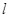 与曲线C交于 B、D两点,求
与曲线C交于 B、D两点,求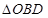 面积的最大值.
面积的最大值.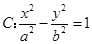 的右顶点作
的右顶点作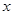 轴的垂线与
轴的垂线与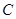 的一条渐近线相交于
的一条渐近线相交于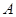 .若以
.若以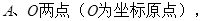 ,则双曲线
,则双曲线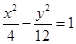 B.
B.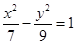 C.
C.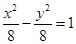 D.
D.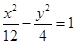
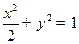 ,
, 为坐标原点,椭圆的右准线与
为坐标原点,椭圆的右准线与 轴的交点是
轴的交点是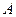 .
.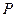 在已知椭圆上,动点
在已知椭圆上,动点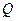 满足
满足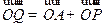 ,求动点
,求动点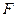 的直线与椭圆交于点
的直线与椭圆交于点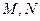 ,求
,求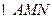 的面积的最大值
的面积的最大值 、
、 为椭圆
为椭圆 的左右焦点,点
的左右焦点,点 为其上一点,且有
为其上一点,且有
 .
.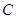 的标准方程;
的标准方程; 与椭圆
与椭圆 交于
交于 、
、 两点,过
两点,过 与椭圆
与椭圆 两点,求四边形
两点,求四边形 的面积
的面积 的最大值.
的最大值.