题目内容
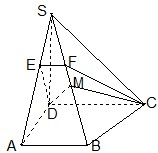 在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=
在直角梯形ABCD中,∠A=∠D=90°,AB<CD,SD⊥平面ABCD,AB=AD=a,S D=| 2 |
(1)求证:四边形EFCD为直角梯形;
(2)设SB的中点为M,当
| CD |
| AB |
分析:(1)由CD∥AB,AB?平面SAB,知CD∥平面SAB,面EFCD∩面SAB=EF,CD∥EF.由∠D=90°,知CD⊥AD,SD⊥面ABCD.由此能够证明EFCD为直角梯形.
(2)由题中条件可推得DM⊥SB,当
=2时,△DMC为直角三角形.由AB=a,知CD=2a,BD=
=
a,∠BDC=450,SD⊥平面ABCD,SD⊥BC,BC⊥平面SBD.由此结合几何知识进行求解.
(2)由题中条件可推得DM⊥SB,当
| CD |
| AB |
| AB2+AD2 |
| 2 |
解答:解:(1)∵CD∥AB,AB?平面SAB,
∴CD∥平面SAB
面EFCD∩面SAB=EF,
∴CD∥EF.
∵∠D=90°,
∴CD⊥AD,
又SD⊥面ABCD,
∴SD⊥CD,
∴CD⊥平面SAD,
∴CD⊥ED又EF<AB<CD,
∴EFCD为直角梯形.
(2)当
=2时,能使DM⊥MC.
∵AB=a,
∴CD=2a,BD=
=
a,∠BDC=450,
∴BC=
a,BC⊥BD,
∴SD⊥平面ABCD,
∴SD⊥BC,
∴BC⊥平面SBD.
在△SBD中,SD=DB,M为SB中点,
∴MD⊥SB.
∴MD⊥平面SBC,MC?平面SBC,
∴MD⊥MC,
∴△DMC为直角三角形.
∴CD∥平面SAB
面EFCD∩面SAB=EF,
∴CD∥EF.
∵∠D=90°,
∴CD⊥AD,
又SD⊥面ABCD,
∴SD⊥CD,
∴CD⊥平面SAD,
∴CD⊥ED又EF<AB<CD,
∴EFCD为直角梯形.
(2)当
| CD |
| AB |
∵AB=a,
∴CD=2a,BD=
| AB2+AD2 |
| 2 |
∴BC=
| 2 |
∴SD⊥平面ABCD,
∴SD⊥BC,
∴BC⊥平面SBD.
在△SBD中,SD=DB,M为SB中点,
∴MD⊥SB.
∴MD⊥平面SBC,MC?平面SBC,
∴MD⊥MC,
∴△DMC为直角三角形.
点评:本题考查棱锥的结构特征,解题时要认真审题,仔细解答,注意空间几何体的合理转化.

练习册系列答案
相关题目
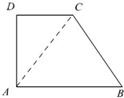
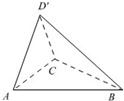
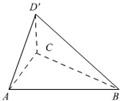
 (2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
(2011•盐城二模)如图,在直角梯形ABCD中,AB⊥AD,AD=DC=1,AB=3,动点P在△BCD内运动(含边界),设
 如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD=
如图,在直角梯形ABCD中,∠BAD=90°,AD∥BC,AB=2,AD= 如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为
如图,在直角梯形ABCD中,AB∥CD,AB⊥BC,AB=1,CD=3,S△BCD=6,则梯形ABCD的面积为