题目内容
设函数
曲线y=f(x)通过点（0，2a+3），且在点（－1，f（－1））处的切线垂直于y轴.
（Ⅰ）用a分别表示b和c；
（Ⅱ）当bc取得最小值时，求函数g(x)= 
的单调区间.
(Ⅰ)因为
又因为曲线
通过点（0，2a+3）,
故
又曲线在（-1，f(-1)）处的切线垂直于y轴，故
即-2a+b=0,因此b=2a.
(Ⅱ)由(Ⅰ)得
故当
时，
取得最小值-
.
此时有
从而
所以
令
，解得
当
当
当
由此可见，函数
的单调递减区间为（-∞，-2）、（2，+∞）；单调递增区间为（-2，2）.
练习册系列答案
相关题目
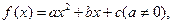曲线y=f(x)通过点（0，2a+3），且
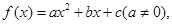曲线y=f(x)通过点（0，2a+3），且
曲线y=f(x)通过点（0，2a+3），且在点（-1，f（-1））
曲线y=f(x)通过点（0，2a+3），且在点（-1，f（-1））
曲线y=f(x)通过点（0，2a+3），且在点（-1，f（-1））