题目内容
已知函数 .
.(I)求
 的值;
的值;(II)求函数f(x)的最小正周期及单调递减区间.
【答案】分析:(I)把x=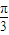 直接代入函数的解析式,化简求得f(
直接代入函数的解析式,化简求得f(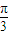 )的值.
)的值.
(II)由cosx≠0,得 x≠kπ+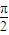 ,(k∈z ).化简函数的解析式为sin(2x+
,(k∈z ).化简函数的解析式为sin(2x+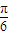 ),从而求得f(x)的最小正周期.再由2kπ+
),从而求得f(x)的最小正周期.再由2kπ+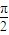 ≤2x+
≤2x+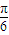 ≤2kπ+
≤2kπ+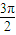 ,x≠kπ+
,x≠kπ+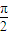 ,k∈z,求得x的范围,即可求得函数的减区间.
,k∈z,求得x的范围,即可求得函数的减区间.
解答:解:(I)由函数的解析式可得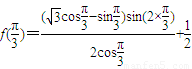
=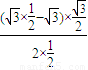 +
+ =0+
=0+ =
= .…(4分)
.…(4分)
(II)∵cosx≠0,得 x≠kπ+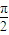 ,(k∈z )
,(k∈z )
故f(x)的定义域为{x|x≠kπ+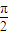 ,(k∈z )}.
,(k∈z )}.
因为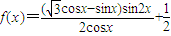 =sinx(
=sinx(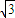 cosx-sinx)+
cosx-sinx)+ =
=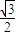 sin2x-sin2x+
sin2x-sin2x+
=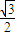 sin2x-
sin2x-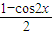 +
+ =
=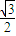 sin2x+
sin2x+ cos2x=sin(2x+
cos2x=sin(2x+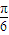 ),
),
所以f(x)的最小正周期为 T=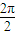 =π.
=π.
由2kπ+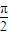 ≤2x+
≤2x+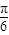 ≤2kπ+
≤2kπ+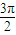 ,x≠kπ+
,x≠kπ+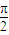 ,k∈z,
,k∈z,
得 kπ+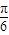 ≤x≤kπ+
≤x≤kπ+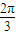 ,x≠kπ+
,x≠kπ+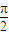 ,k∈z,
,k∈z,
所以,f(x)的单调递减区间为 (kπ+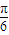 ,kπ+
,kπ+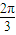 ),(kπ+
),(kπ+ ,kπ+
,kπ+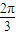 ),k∈z.…(13分)
),k∈z.…(13分)
点评:本题主要考查二倍角公式、两角和差的正弦公式、正弦函数的单调性,属于中档题.
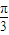 直接代入函数的解析式,化简求得f(
直接代入函数的解析式,化简求得f(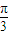 )的值.
)的值.(II)由cosx≠0,得 x≠kπ+
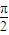 ,(k∈z ).化简函数的解析式为sin(2x+
,(k∈z ).化简函数的解析式为sin(2x+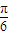 ),从而求得f(x)的最小正周期.再由2kπ+
),从而求得f(x)的最小正周期.再由2kπ+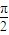 ≤2x+
≤2x+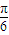 ≤2kπ+
≤2kπ+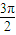 ,x≠kπ+
,x≠kπ+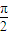 ,k∈z,求得x的范围,即可求得函数的减区间.
,k∈z,求得x的范围,即可求得函数的减区间.解答:解:(I)由函数的解析式可得
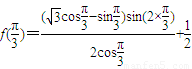
=
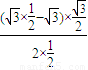 +
+ =0+
=0+ =
= .…(4分)
.…(4分)(II)∵cosx≠0,得 x≠kπ+
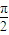 ,(k∈z )
,(k∈z ) 故f(x)的定义域为{x|x≠kπ+
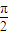 ,(k∈z )}.
,(k∈z )}.因为
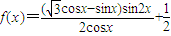 =sinx(
=sinx(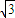 cosx-sinx)+
cosx-sinx)+ =
=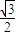 sin2x-sin2x+
sin2x-sin2x+
=
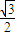 sin2x-
sin2x-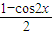 +
+ =
=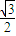 sin2x+
sin2x+ cos2x=sin(2x+
cos2x=sin(2x+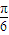 ),
),所以f(x)的最小正周期为 T=
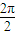 =π.
=π.由2kπ+
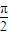 ≤2x+
≤2x+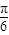 ≤2kπ+
≤2kπ+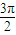 ,x≠kπ+
,x≠kπ+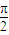 ,k∈z,
,k∈z,得 kπ+
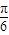 ≤x≤kπ+
≤x≤kπ+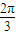 ,x≠kπ+
,x≠kπ+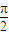 ,k∈z,
,k∈z,所以,f(x)的单调递减区间为 (kπ+
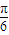 ,kπ+
,kπ+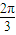 ),(kπ+
),(kπ+ ,kπ+
,kπ+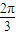 ),k∈z.…(13分)
),k∈z.…(13分)点评:本题主要考查二倍角公式、两角和差的正弦公式、正弦函数的单调性,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 ,
, 的单调区间;
的单调区间; 上的最小值。
上的最小值。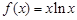 。
。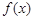 的最小值;
的最小值;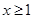 都有
都有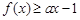 ,求实数
,求实数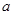 的取值范围。
的取值范围。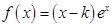 ,
,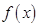 的单调区间;(II)求
的单调区间;(II)求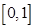 上的最小值。
上的最小值。 。
。 的单调区间;
的单调区间; 成立,求实数
成立,求实数 的取值范围。
的取值范围。