题目内容
(本小题满分12分)已知函数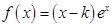 ,
,
(I)求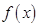 的单调区间;(II)求
的单调区间;(II)求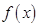 在区间
在区间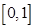 上的最小值。
上的最小值。
【答案】
(Ⅰ)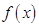 在
在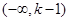 上递减,在
上递减,在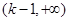 上递增;(Ⅱ)
上递增;(Ⅱ)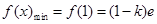
【解析】
试题分析: (1)根据函数的导数以及函数的单调性的关系得到结论。
(2)对于参数k-1是否为零,来分情况讨论得到结论,判定函数单调性,得到结论。
解:(Ⅰ)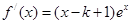 ,令
,令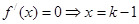 ;所以
;所以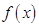 在
在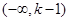 上递减,在
上递减,在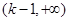 上递增;
上递增;
(Ⅱ)当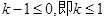 时,函数
时,函数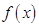 在区间
在区间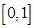 上递增,所以
上递增,所以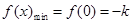 ;
;
当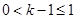 即
即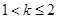 时,由(Ⅰ)知,函数
时,由(Ⅰ)知,函数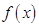 在区间
在区间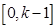 上递减,
上递减, 上递增,所以
上递增,所以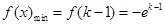 ;
;
当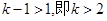 时,函数
时,函数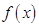 在区间
在区间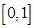 上递减,所以
上递减,所以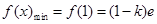
考点:本题主要考查了导数在研究函数中的运用。
点评:解决该试题的关键是利用导数的正负与函数单调性的关系,判定函数单调性,进而得到极值,并比较端点值的大小,得到最值。

练习册系列答案
相关题目