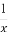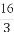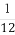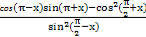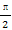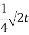题目内容
已知sinθ,cosθ是关于x的方程x2-ax+a=0(a∈R)的两个根.
(1)求cos3(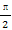 -θ)+sin3(
-θ)+sin3(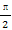 -θ)的值.
-θ)的值.
(2)求tan(π-θ)-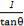 的值.
的值.
(1) 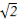 -2 (2) 1+
-2 (2) 1+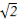
【解析】【思路点拨】先由方程根的判别式Δ≥0,求a的取值范围,而后应用根与系数的关系及诱导公式求解.
【解析】
由已知,原方程的判别式Δ≥0,即(-a)2-4a≥0,∴a≥4或a≤0.
又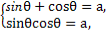
(sinθ+cosθ)2=1+2sinθcosθ,
则a2-2a-1=0,从而a=1-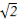 或a=1+
或a=1+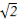 (舍去),
(舍去),
因此sinθ+cosθ=sinθcosθ=1-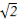 .
.
(1)cos3( -θ)+sin3(
-θ)+sin3( -θ)=sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθ·
-θ)=sin3θ+cos3θ=(sinθ+cosθ)(sin2θ-sinθ·
cosθ+cos2θ)=(1-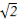 )[1-(1-
)[1-(1-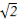 )]=
)]=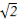 -2.
-2.
(2)tan(π-θ)-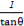 =-tanθ-
=-tanθ-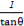 =-(
=-( +
+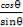 )=-
)=-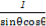 =-
=-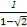 =1+
=1+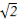 .
.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目