Question

（2012•淄博一模）设方程log₄x-（

1

4

）^x=0、log 

1

4

x-（

1

4

）^x=0的根分别为x₁、x₂，则（　　）

A．0＜x₁ x₂＜1

B．x₁ x₂=1

C．1＜x₁ x₂＜2

D．x₁ x₂≥2

Answer 1

分析：由题意可得，函数y=log₄x和函数y=（

1

4

）^x交点的横坐标为x₁，函数y=log 

1

4

x和函数y=（

1

4

）^x的交点的横坐标为x₂，结合图象可得x₁=

1

2

，1＜x₂＜2，从而得到

1

2

＜x₁x₂＜1，由此求得答案．⑤

解答：解：∵方程log₄x-（

1

4

）^x=0、log 

1

4

x-（

1

4

）^x=0的根分别为x₁、x₂，
∴log₄x=（

1

4

）^x，且log 

1

4

x=（

1

4

）^x，
故函数y=log₄x和函数y=（

1

4

）^x交点的横坐标为x₁，函数y=log 

1

4

x和函数y=（

1

4

）^x的交点的横坐标为x₂，

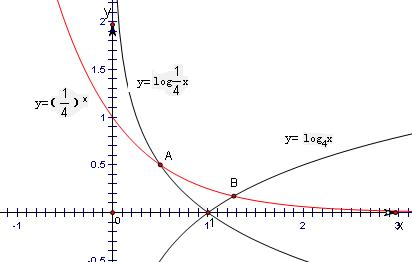
结合图象可得x₁=

1

2

，1＜x₂＜2，∴

1

2

＜x₁x₂＜1，
故选A．

点评：本题考查了根的存在性及根的个数判断，以及函数与方程的思想，解答关键是运用数形结合的思想，属于中档题．