题目内容
以过椭圆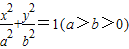
的右焦点的弦为直径的圆与直线
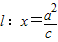的位置关系是（ ）A．相交
B．相切
C．相离
D．不能确定
【答案】分析：过弦的端点作右准线的垂线求出圆心到准线的距离，再与圆的半径比较，即可判断圆与直线的位置关系．
解答：解：设过椭圆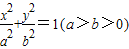
的右焦点的弦为AB，右焦点为F
令圆半径为r，则r=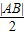
分别过点A，B做右准线的垂线，则构成一个直角梯形，两底长分别为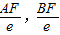
（e为离心率）
圆心到准线的距离d为梯形的中位线长即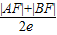
=
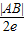
∵0＜e＜1
∴
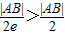
∴d＞r
∴过椭圆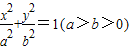
的右焦点的弦为直径的圆与直线
相离
点评：本题重点考查直线与圆的位置关系，考查椭圆的定义，解题的关键是求出圆心到直线的距离．
解答：解：设过椭圆
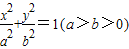的右焦点的弦为AB，右焦点为F令圆半径为r，则r=
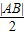
分别过点A，B做右准线的垂线，则构成一个直角梯形，两底长分别为
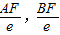（e为离心率）圆心到准线的距离d为梯形的中位线长即
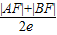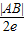
=∵0＜e＜1
∴
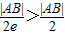
∴d＞r
∴过椭圆
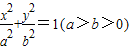的右焦点的弦为直径的圆与直线相离点评：本题重点考查直线与圆的位置关系，考查椭圆的定义，解题的关键是求出圆心到直线的距离．
练习册系列答案
相关题目
经过点
，离心率为
，动点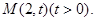
截得的弦长为2的圆的方程；
的右焦点的弦为直径的圆与直线
的位置关系是
经过点
，离心率是
，动点
（1）求椭圆的标准方程 
截得
的右焦点为焦点F．