题目内容
11．某学生参加3门课程的考试．假设该学生第一门、第二门及第三门课程取得合格水平的概率依次为$\frac{4}{5}$，$\frac{3}{5}$，$\frac{2}{5}$，且不同课程是否取得合格水平相互独立．则该生只取得一门课程合格的概率为$\frac{37}{125}$．分析 分别求出只有第一门合格的概率、只有第二门合格的概率、只有第三门合格的概率，相加，即得所求．
解答 解：只有第一门合格的概率等于$\frac{4}{5}$（1-$\frac{3}{5}$）（1-$\frac{2}{5}$），
只有第二门合格的概率等于（1-$\frac{4}{5}$）•$\frac{3}{5}$（1-$\frac{2}{5}$），
只有第三门合格的概率等于（1-$\frac{4}{5}$）（1-$\frac{3}{5}$）•$\frac{2}{5}$，
故该生只取得一门课程合格的概率为$\frac{4}{5}$（1-$\frac{3}{5}$）（1-$\frac{2}{5}$）+（1-$\frac{4}{5}$）•$\frac{3}{5}$（1-$\frac{2}{5}$）+（1-$\frac{4}{5}$）（1-$\frac{3}{5}$）•$\frac{2}{5}$=$\frac{37}{125}$．
故答案为：$\frac{37}{125}$．
点评 本题主要考查相互独立事件的概率乘法公式的应用，体现了分类讨论的数学思想，属于中档题．
练习册系列答案
全优考典单元检测卷及归类总复习系列答案
相关题目
19．从4个不同的独唱节目和2个不同的合唱节目中选出4个节目编排一个节目单，要求最后一个节目必须是合唱，则这个节目单的编排方法共有（ ）
| A． | 14种 | B． | 48种 | C． | 72种 | D． | 120种 |
6．
如图，已知直线l⊥平面α，垂足为O，在△ABC中，BC=2，AC=2，AB=2$\sqrt{2}$，点P是边AC的中点．该三角形在空间按以下条件作自由移动：
（1）A∈l，（2）C∈α．则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为（ ）
如图，已知直线l⊥平面α，垂足为O，在△ABC中，BC=2，AC=2，AB=2$\sqrt{2}$，点P是边AC的中点．该三角形在空间按以下条件作自由移动：（1）A∈l，（2）C∈α．则|$\overrightarrow{OP}$+$\overrightarrow{PB}$|的最大值为（ ）
| A． | 2 | B． | 2$\sqrt{2}$ | C． | 1+$\sqrt{5}$ | D． | $\sqrt{10}$ |
16．在正方形ABCD中，已知AB=3，E是CD中点，那么$\overrightarrow{AE}\;•\;\overrightarrow{BD}$等于（ ）
| A． | $\frac{27}{2}$ | B． | 6 | C． | $\frac{9}{2}$ | D． | $\frac{7}{2}$ |
3．设数列{an}的前n项和为Sn，若an+Sn=1，则a4=（ ）
| A． | $\frac{1}{8}$ | B． | $\frac{1}{16}$ | C． | $\frac{1}{32}$ | D． | $\frac{1}{64}$ |
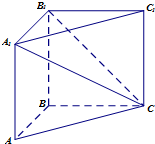如图所示：在直三棱柱ABC-A1B1C1中，AB⊥BC，AB=BC=BB1，则平面A1B1C与平面ABC所成的二面角的大小为$\frac{π}{4}$．