题目内容
【题目】如图,互相垂直的两条公路AP、AQ旁有一矩形花园ABCD,现欲将其扩建成一个更大的三角形花园AMN,要求点M在射线AP上,点N在射线AQ上,且直线MN过点C,其中AB=36米,AD=20米.记三角形花园AMN的面积为S. (Ⅰ)问:DN取何值时,S取得最小值,并求出最小值;
(Ⅱ)若S不超过1764平方米,求DN长的取值范围.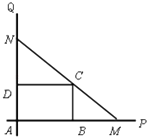
【答案】解:(Ⅰ)设DN=x米(x>0),则AN=x+20. 因为DC∥AB,所以△NDC∽△NAM
所以 ![]() ,
,
所以 ![]() ,即
,即 ![]() .
.
所以 ![]()
= ![]() ,当且仅当x=20时取等号.
,当且仅当x=20时取等号.
所以,S的最小值等于1440平方米.
(Ⅱ)由 ![]() 得x2﹣58x+400≤0.
得x2﹣58x+400≤0.
解得8≤x≤50.
所以,DN长的取值范围是[8,50]
【解析】(Ⅰ)由于DC∥AB得出△NDC∽△NAM,从而AN,AM用DN表示,利用三角形的面积公式表示出面积,再利用基本不等式求最值,注意等号何时取得.(Ⅱ)由S不超过1764平方米,建立不等式,从而可求DN长的取值范围.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目