题目内容
已知二次函数f(x)=ax2+bx-3在x=1处取得极值,且在(0,-3)点处的切线与直线2x+y=0平行.(Ⅰ)求f(x)的解析式;
(Ⅱ)求函数g(x)=xf(x)+4x的单调递增区间.
分析:(1)先对函数f(x)求导,令f'(1)=0,f'(0)=-2即可得到答案.
(2)将函数f(x)的解析式代入求出函数g(x)的解析式后求导,令导函数大于0求出x的范围即可.
(2)将函数f(x)的解析式代入求出函数g(x)的解析式后求导,令导函数大于0求出x的范围即可.
解答:解:(Ⅰ)由f(x)=ax2+bx-3,可得f′(x)=2ax+b.
由题设可得
即
解得a=1,b=-2.
所以f(x)=x2-2x-3.
(Ⅱ)由题意得g(x)=xf(x)+4x=x3-2x2+x,
所以g′(x)=3x2-4x+1=(3x-1)(x-1).
令g′(x)=0,得x1=
,x2=1.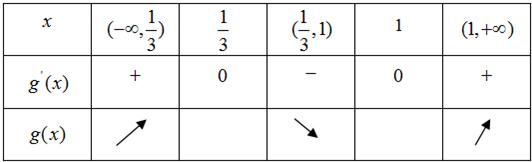
所以函数g(x)的单调递增区间为(-∞,
),(1,+∞).
由题设可得
|
|
解得a=1,b=-2.
所以f(x)=x2-2x-3.
(Ⅱ)由题意得g(x)=xf(x)+4x=x3-2x2+x,
所以g′(x)=3x2-4x+1=(3x-1)(x-1).
令g′(x)=0,得x1=
| 1 |
| 3 |

所以函数g(x)的单调递增区间为(-∞,
| 1 |
| 3 |
点评:本题主要考查导数的几何意义、导数的正负情况和原函数的增减性的关系.属基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目